Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 11.Problemas - Ex. 17
A partir da tabela da pág. 265, tratando o hélio gasoso como um gás de Van der Waals calcule o diâmetro efetivo de um átomo de hélio. Compare o resultado com aquele obtido no problema . Discuta a razão da concordância ou discrepância.
Tabela da pág. 265:
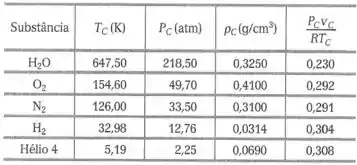
Passo 1
Vamos começar lembrando da equação de Van der Waals:
Ok, pense o seguinte: qual grandeza nessa equação pode definir o diâmetro do átomo de hélio?
O segredo aqui é lembrar do significado da constante ! Ela representa o volume de exclusão de um mol do gás.
Dá uma olhada nesse desenho que representa o volume de exclusão de um único átomo:
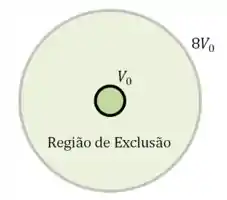
Esse volume de exclusão define uma região em que não pode haver outros átomos, e em geral é oito vezes o volume do átomo.
E para um mol de gás, temos que multiplicar pelo número de Avogadro, então:
Só um detalhe: no modelo de Van der Waals, só se considera uma metade da esfera no volume exclusão, então:
Passo 2
Agora temos que dar um jeito de encontrar o valor de .
A tabela do enunciado deu os valores de e . As fórmulas dessas duas constantes são as seguintes:
Se você dividir uma pela outra, vai encontrar o seguinte:
Beleza, agora é só substituir com os valores da tabela e da constante :
Então:
Passo 3
Voltando na fórmula que escrevemos lá no passo :
E substituindo os valores:
Então o diâmetro é:
Quando resolvemos o problema 13, o valor encontrado foi:
Ou seja, temos uma discrepância. Mas a razão pra isso é bem clara! No exercício 13, a temperatura era:
E agora estamos trabalhando com a temperatura crítica, que é:
Ou seja, é uma temperatura muito mais baixa, em que a precisão do modelo de Van der Waals é muito pior.
Resposta
O diâmetro efetivo do gás do hélio seria . O valor é diferente do calculado no problema 13 devido às diferenças extremas de temperatura entre os dois casos.