Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 76
Uma pedra de é rodada em um círculo horizontal na ponta de uma corda de . A corda faz um ângulo de com a horizontal. Determine a rapidez da pedra.
Passo 1
Olá, querido! Cê tá bem? Temos uma situação assim:
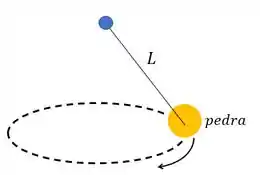
A ideia é a gente achar a rapidez dessa pedrinha em movimento circular.
Vamos usar um esquema para representar as forças que agem sobre a pedra:
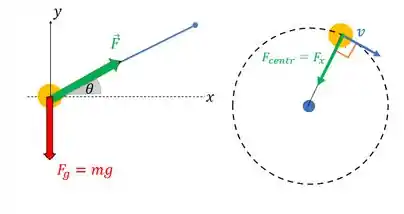
As componentes de são:
Percebe que para que haja uma trajetória circular, é necessário que acha uma força no plano da circunferência apontando para o centro da trajetória. Quem vai fazer esse papel é , porque o movimento da pedra só ocorre na horizontal.
A ideia é que a pedra gire apenas em um plano horizontal, ou seja, sem nenhum movimento no eixo , por isso queremos que haja equilíbrio na vertical. Pela segunda lei de Newton:
Passo 2
E na direção horizontal temos as forças que mantém a trajetória circular. Aplicando a segunda lei de Newton para direção :
Mas lembra que esse é a aceleração horizontal da força resultante sobre a pedra. Só que na horizontal temos um movimento circular e força resultante é uma força centrípeta, então a aceleração horizontal é a aceleração centrípeta, que é dada por . Substituindo:
Substituindo isso na equação final do passo anterior:
Passo 3
Agora vamos resolver essa equação para calcular a rapidez :
Antes de substituir os valores numéricos precisamos nos lembrar de que o raio da trajetória circular não é igual ao comprimento da corda, e sim a projeção do comprimento dela na horizontal, já que a trajetória é só horizontal:
E então:
Substituindo os dados:
Resposta
A rapidez da pedra é .