Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 80
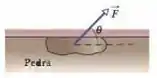
Uma pedra de é deslocada em contato com o teto horizontal de uma caverna (Fig. 6-48). Se o coeficiente de atrito cinético é e a força aplicada à pedra faz um ângulo para cima com a horizontal, qual deve ser o módulo para que a pedra se mova com velocidade constante?
Passo 1
Oláaa, querido! Tá bem?
Então, a pedra está sendo arrastada pelo teto. Aí ele quer saber o módulo da força para que a pedra tenha velocidade constante. Ou seja, para que não haja aceleração horizontal
Então galera, a primeira coisa que devemos fazer é construir o diagrama de corpo livre da pedra :
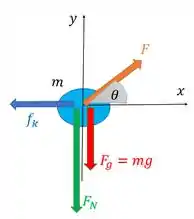
Repara que a força normal está para baixo, já que a superfície de contato agora é o teto. E repara que a força de atrito é a de atrito cinético porque há movimento e ela vale
Agora vamos lá aplicar a segunda lei de Newton e achar !
Passo 2
De acordo com a 2° Lei de Newton no eixo x para a pedra, vamos ter
Como , então:
Aí nessa direção, a gente temos , no sentido negativo se opondo a tendência de movimento. E temos também a componente de que é dada por que aponta para positivo.
O somatório de forças fica
Passo 3
Agora a segunda lei de Newton para esse mesmo bloco para a direção , sabendo que pois não há movimento nessa direção
Nessa direção temos a força normal e a força peso apontando para a parte negativa e a componente de para cima. O somatório fica:
Passo 4
Temos as equações:
Como queremos , vamos isolar na primeira e substituir na segunda:
Isolando
Para , e , obtemos .
Resposta
Tranquilo pessoal ??? Bora resolver mais questões então