Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 17
Bonnie e Clyde arrastam um cofre de banco de sobre o piso em direção ao carro de fuga. O cofre é arrastado com uma velocidade constante se Clyde o empurra por trás com de força enquanto Bonnie o puxa para a frente por meio de uma corda com de força. Qual é o coeficiente de atrito cinético do cofre sobre o piso da agência bancária?
Passo 1
Antes de tudo vamos fazer um diagrama de corpo livre pra esse cofre de banco:
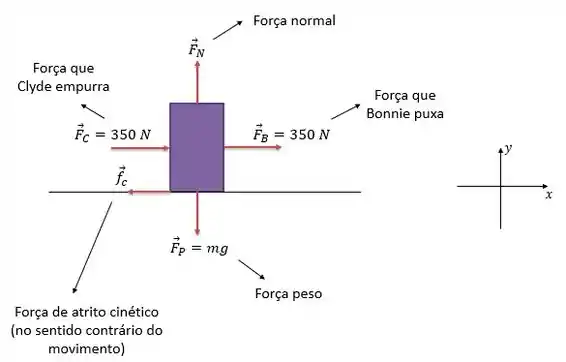
Prontinho! Agora fica bem mais fácil de visualizar as forças que atuam sobre o corpo né? E coloquei ali do ladinho também as direções e que vamos considerar, belezinha?
Passo 2
Agora vamos analisar tudo isso.
A questão nos diz que nessa situação a velocidade do cofre é constante, então o somatório de forças na direção , que é a direção na qual o cofre se movimenta, tem que ser zero:
Como conhecemos o módulo de e , podemos achar o módulo da força de atrito cinético, :
Além disso, o bloco não se movimenta na direção , então o somatório nas forças na direção também tem que ser zero:
A partir disso podemos achar o módulo da força normal:
A questão nos fornece , a massa do cofre, e a aceleração da gravidade é conhecida:
Logo:
Passo 3
Ai tu pensa: Porque estamos fazendo isso? Não estamos chegando em lugar nenhum 
Aí que você se engana. Lembra da fórmula da força de atrito cinético?
Já achamos o módulo da força de atrito cinético e o modulo da força normal, nossa única incógnita é o coeficiente de atrito cinético, que é o que a questão pede:
