Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 23.Exercício - Ex. 5

Uma pequena esfera metálica, com uma carga líquida q 1 =   - 2,8   μ C é mantida em repouso por suportes isolantes. Uma segunda esfera metálica, com uma carga líquida q 2 =   - 7,8   μ C e massa igual a 1,5   g é projetada contra q 1 . Quando as distâncias entre as duas esferas é igual a 0,800   m , q 2 se aproxima de q 1 com velocidade de 22   m / s . Suponha que as duas esferas possam ser tratadas como cargas puntiformes. Despreze a gravidade. a)Qual é a velocidade da carga q 2 quando a distância entre as duas esferas é de 0,400   m ? b)Qual será a menor distância entre q 2 e q 1 ?

Passo 1

letra a)

Pela conservação de energia temos que:

K a + U a = K b + U b

O ponto a é o ponto onde a carga q 2 está a 0,8 m da carga q 1 e o ponto b é o ponto onde a carga q 2 está a 0,4 m da carga q 1 .

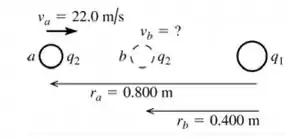
Passo 2

Queremos então a velocidade v b .

1 2 m v b 2 = Δ U + K a

1 2 m v b 2 = U a - U b + K a

Precisamos agora encontrar as energias potenciais para achar a velocidade.

Passo 3

Substituindo a expressão da energia, temos que:

U a - U b = 1 4 π ϵ o q 1 q 2 a - 1 4 π ϵ o q 1 q 2 b

U a - U b = 1 4 π 8,66 ⋅ 10 - 12 - 2,8 ⋅ 10 - 6 - 7,8 ⋅ 10 - 6 0,8 - 1 4 π 8,66 ⋅ 10 - 12 - 2,8 ⋅ 10 - 6 - 7,8 ⋅ 10 - 6 0,4

U a - U b = - 0,2453   J

Passo 4

A energia cinética no ponto a será:

K a = 1 2 m v a 2

K a = 1 2 1,5 ⋅ 10 - 3 22 2

K a = 0,3630   J

Passo 5

A velocidade v b será:

1 2 m v b 2 = - 0,2453 + 0,3630

1 2 m v b 2 = 0,1177

v b = 2 ⋅ 0,1177 1,5 ⋅ 10 - 3

v b = 12,5   m / s

Passo 6

letra b)

A menor distância será quando a velocidade final for nula.

Pela conservação de energia temos que:

K a + U a = U c

Já sabemos do item anterior a energia cinética e potencial no ponto a .

U c = 0,3630 + 0,2454

U c = 0,6084   J

Passo 7

Calculando a distância partir da energia potencial, temos que:

U c = 1 4 π ϵ o q 1 q 2 c

c = 4 π ϵ o U c q 1 q 2

c = 4 π 8,66 ⋅ 10 - 12 ⋅ 0,6084 - 2,8 ⋅ 10 - 6 - 7,8 ⋅ 10 - 6

c = 0,323   m

Resposta

letra a) v b = 12,5   m / s

letra b) c = 0,323   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma carga puntiforme Q = + 4,6μ C é mantida em repouso na origem. Uma segunda carga puntiforme q = + 1,2μ C com massa igual a 2,80 ⋅ 10 - 4k g é colocada sobre o eixo O x a uma distância de 0,250m da
Dois prótons são direcionados diretamente um contra o outro por um acelerador cíclotron, com velocidade escalar de 1000 km/s, medida em relação à Terra. Determine a força elétrica que esses prótons ex
Suponha que, em um relâmpago, a diferença de potencial entre uma nuvem e a terra é 1,0×10 9V e a carga transferida pelo relâmpago é 30C . ( a ) Qual é a variação da energia da carga transferida? ( b )
Se o potencial elétrico é uniforme em uma região do espaço, o que pode ser dito sobre o campo elétrico nesta região?
Um próton é deslocado para a esquerda em um campo elétrico uniforme que aponta para a direita. O próton está se movendo no sentido que o potencial aumenta ou diminui? A energia potencial eletrostática