Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.4 - Ex. 54

Um pequeno botão sobre uma plataforma circulante horizontal com diâmetro de 0,320 m gira junto com a plataforma com 40,0 rev/min, desde que o botão não esteja a uma distância maior do que 0,150 m do eixo. a) Qual é o coeficiente de atrito estático entre o botão e a plataforma? b) Qual é a distância máxima ao eixo da plataforma que o botão pode ser colocado sem que ele deslize, se a plataforma gira com 60,0 rev/min?

Passo 1

O botão se move em um círculo, por isso tem aceleração centrípeta, a c e n t r , direcionada para o centro do círculo.

Sabemos que a aceleração centrípeta é:

a c e n t r = v 2 R

Temos que o diâmetro é d = 0,320 m , então o raio se dá por: R = d 2 = 0,320 m 2 = 0,160 m .

Vamos esboçar um diagrama do corpo livre para o botão:

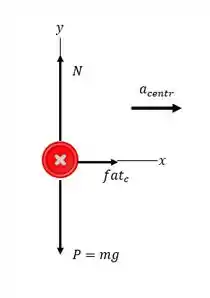
Passo 2

Vamos aplicar a 2º Lei de Newton para o botão:

Para o e i x o   x :

∑ F x = m a x

f a t = m a c e n t r = m ⋅ v 2 R

Passo 3

No e i x o   y :

∑ F y = m a y

F y = N + - m g = 0

⇒ N = m g

Passo 4

  1. Sabemos que a força de atrito se dá por: f a t = μ c ⋅ N = μ c m g .   Então temos que:

μ c m g = m ⋅ v 2 R

⇒   μ c = v 2 R g

E expressando a velocidade linear v em termos da velocidade angular ω , obtemos:

v = ω R

⇒   μ c = ω 2 R 2 R g

⇒   μ c = ω 2 R g

Passo 5

Dado que ω = 40   rev / min , passando para rad /s , teremos que:

ω = 40 × 2 π 60

ω = 4,2   rad/s

Então podemos calcular o coeficiente de atrito cinético:

μ c = 4,2   rad/s 2 × 0,150   m 9,8   m/s²

μ c = 0,2 7

Passo 6

Para o mesmo coeficiente de atrito estático, o raio máximo é proporcional ao quadrado do período (períodos mais longos significam velocidades mais lentas, então o botão pode ser movido mais para fora) e, portanto, é inversamente proporcional a o quadrado da velocidade. Assim, na velocidade mais alta, o raio máximo é:

0,150 m ⋅ 40 60 2 = 0,067   m

Resposta

  1. μ c = 0,2 7
  2. 0,067   m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma curva plana (não compensada com inclinação lateral) de uma estrada possui raio igual a 220,0m . Um carro contorna a curva com uma velocidade de 25,0m / s . a) Qual é o coeficiente de atrito mínimo
Uma mulher de 50,0 kg pilota um avião mergulhando verticalmente para baixo e muda o curso para cima, de modo que o avião passa a descrever um círculo vertical. a) Se a velocidade do avião na base do c
Um problema para a vida humana no espaço exterior é o peso aparente igual a zero. Um modode contornar o problema seria fazer a estação espacial girar em torno do centro com uma taxa constante. Isso cr
Um carro de 1125 kg e uma caminhonete de 2250 kg se aproximam de uma curva na estrada que possui raio 225 m. a) A que ângulo o engenheiro deve inclinar essa curva, de modo queveículos com deslocamento