Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.4 - Ex. 51
Um carro de 1125 kg e uma caminhonete de 2250 kg se aproximam de uma curva na estrada que possui raio 225 m. a) A que ângulo o engenheiro deve inclinar essa curva, de modo que
veículos com deslocamento de 65,0 mi/h possam contorná-la com segurança, seja qual for o estado dos pneus? A caminhonete mais pesada deve seguir mais lentamente do que o carro mais leve? b) Considerando que o carro e a caminhonete fazem a curva a 65,0 mi/h, ache a força normal sobre cada veículo em função da superfície da estrada.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que um carro de e uma caminhonete de se aproximam de uma curva na estrada que possui raio .
Queremos calcular o ângulo em que o o engenheiro deve inclinar essa curva de modo que
veículos com deslocamento de possam contorná-la com segurança.
Para isso, devemos decompor as forças que atuam no veículo quando este passa pela curva e aplicar a segunda Lei de Newton:
Onde é a força resultante, é massa e é a aceleração.
Também queremos encontrar a força normal sobre cada veículo em função da superfície da estrada dado que o carro e a caminhonete fazem a curva a .
Para isso, também utilizaremos o diagrama de corpo livre que vamos fazer para decompor as forças.
Passo 2
Vamos assumir o atrito insignificante... então as únicas duas forças que atuam sobre o carro são seu peso e a força normal.
Como a estrada é inclinada, a força normal (que atua perpendicularmente à superfície da estrada) possui um componente horizontal.
Esse componente provoca a aceleração horizontal do carro em direção ao centro da trajetória curva do carro.
Como forças e aceleração estão envolvidas, usaremos a 2º lei de Newton para encontrar o ângulo que chamaremos de .
Vamos esboçar o diagrama de corpo livre nesse caso para visualizarmos melhor:
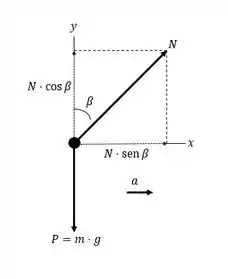
Passo 3
Vamos aplicar a 2º Lei de Newton:
Para o :
Para o :
Substituindo na equação , encontramos uma expressão para o ângulo de inclinação:
Passo 4
E sabemos que:
Onde é a aceleração centrípeta e é a velocidade.
Substituindo essa aceleração na equação do ângulo de inclinação que encontramos, , obtemos:
Passo 5
- Vamos analisar os dados:
Note que: A expressão para não envolve a massa do veículo, para que o caminhão e o carro viajem na mesma velocidade.
Passo 6
Nós encontramos a expressão da força normal, :
Então vamos calcula-la em função do carro e do caminhão.
Para o carro:
Passo 6
Para o caminhão:
Note que a massa do caminhão é o dobro da massa do carro:
Assim,
O componente vertical da força normal deve ser igual ao peso do veículo, de modo que a força é proporcional a massa.