Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.4 - Ex. 58

Uma mulher de 50,0 kg pilota um avião mergulhando verticalmente para baixo e muda o curso para cima, de modo que o avião passa a descrever um círculo vertical. a) Se a velocidade do avião na base do círculo for igual a 95,0 m/s, qual será o raio mínimo do círculo para que a aceleração neste ponto não supere 4,0g? b) Qual é seu peso aparente nesse ponto?

Passo 1

O avião tem um movimento circular,então, temos umas aceleração centrípeta, a c e n t r , direcionada para o centro do círculo.

Sabemos que a aceleração centrípeta é:

a c e n t r = v 2 R

Na parte inferior do mergulho, essa aceleração é para cima.

O peso aparente do piloto é a força normal exercida sobre ela pelo assento em que ela está sentada.

Vamos esboçar o dagrama de corpo livre dessa situação.

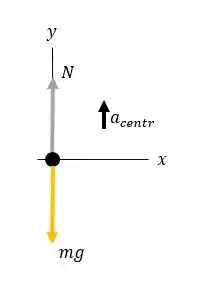
Passo 2

  1. Queremos descobrir o raio, R , desse movimento:

D a d o s :   v = 95 m / s a c e n t r = 4 ⋅ g

Isolando R em: a c e n t r = v 2 R , ficamos com:

R = v 2 a c e n t r

⇒ R = ( 95 m / s ) 2 4 ⋅ 9,8 m / s 2 = 230 m

Passo 3

O peso aparente é dado pela normal, N , então vamos aplicar a segunda lei de Newton no piloto. Bom, pelo nosso diagrama, só há forças atuando no e i x o   y :

∑ F y = m a y

N - m g = m a c e n t r

⇒ N = m ( g + a c e n t r )

N = m g + 4 g = 5 m g = 5 ⋅ 50 k g ⋅ 9,8 m s 2 = 245 0   N

Seu peso aparente é cinco vezes o seu verdadeiro peso, a força da gravidade que a terra exerce sobre ela.

Resposta

  1. R = 230 m
  2. 245 0   N
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um disco de metal de massa m=1,50k g descreve uma circunferência de raio r=20,0c m sobre uma mesa sem atrito enquanto permanece ligado a um cilindro de massa M=2,50k g pendurado por um fio que passa p
Um bonde antigo dobra urna esquina fazendo uma curva plana com 9,1m de raio a 16k m / h . Qual é o ângulo que as alças de mão penduradas no teto fazem com a vertical?
Um passageiro de 85,0k g descreve uma trajetória circular de raio r=3,50m em movimento circular uniforme. (a) A Fig. 6-40a mostra um gráfico do módulo F da força centrípeta em função da velocidade v d
Frear ou desviar? A Fig. 6-44 mostra uma vista superior de um carro que se aproxima de um muro. Suponha que o motorista começa a frear quando a distância entre o carro e o muro é d =107m , que a massa
Ao projetar brinquedos para parques de diversão que fazem movimentos circulares, os engenheiros mecânicos devem levar em conta o fato de que pequenas variações de certos parâmetros podem alterar signi