Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 73
As pernas de um tripé formam ângulos iguais de 90° entre si no vértice, onde elas se juntam. Um bloco de 100 kg está pendurado no vértice. Quais são as forças de compressão sobre as três pernas?
Passo 1
Fala, querido! Temos aqui um tripé que suporta uma carga, e ele quer saber as forças de compressão nas perninhas do tripé. Como assim? Basicamente, o que ele quer são as forças de reação que são produzidas nas pernas do tripé para que a carga não caia no chão.
Vamos fazer um diagrama simples representando a situação:
Nosso objetivo é achar o valor dessas . Como o nosso sistema está paradinho, podemos usar as equações de equilíbrio
Perceba que como estamos em 3D, também temos equilíbrio na direção . A ideia aqui é a gente usar essas equações para achar o valor das em cada perninha do tripé. Vamos!
Passo 2
Antes de aplicar as equações direto, precisamos descobrir a orientação das forças , e daí a gente consegue achar as componentes de cada força para usar nas equações. As forças estão na direção das pernas tripé.
Então a gente vai achar a orientação dessas perninhas. Queremos descobrir o ângulo que cada uma delas faz com a vertical.
Para ajudar, o enunciado diz que cada perna faz um ângulo de com as outras.
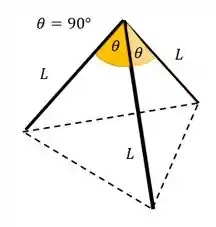
Considerando que cada perna tem comprimento , vemos que isso forma uma espécie de pirâmide no espaço 3D. Cada face dessa pirâmide (formada por cada par de pernas) é um triângulo isósceles desse tipo
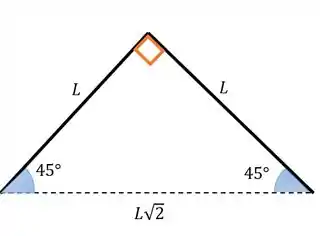
O ângulo entre cada perna vai ser o de como ele falou. E como as pernas são iguais, os outros ângulos serão de . A gente acha essa distância entre os pés fazendo Pitágoras
Com isso a gente tem o comprimento de todas as arestas da pirâmide.
Agora a gente pode partir para achar o ângulo que as pernas fazem com a vertical, que chamamos de na figura ali.
Repara que nós teremos no solo um triangulo equilátero de lado . Como esse triângulo tem todos os lados iguais, todos esses segmentos laranjas serão iguais, assim todas as pernas terão a mesma orientação . Então, o que a gente precisa fazer é achar esse valor .
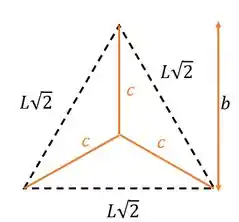
Agora um bizu:
“Para um triângulo equilátero, o ponto do triângulo que é equidistante dos vértices do triângulo é o centroide desse triângulo. E ele fica localizado a dois terços da altura do triângulo, medido do vértice do triângulo”.
Pela nossa figura, isso seria de . Então o que a gente precisa é achar , que é a altura do triângulo. Podemos usar Pitágoras para uma das metades do triângulo.
Logo,
Passo 3
A trigonometria está quase acabando! Só falta nós acharmos o ângulo .
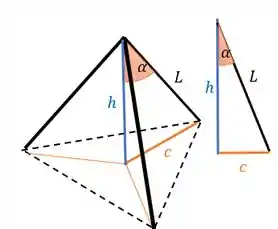
Podemos escrever que
Substituindo e :
Ufaa! Achamos a orientação das perninhas do tripé.
E assim, a orientação das forças! Como vimos que há uma certa simetria, e todas as pernas tem a mesma orientação, todas as forças terão a mesma orientação, e por isso terão módulos iguais.
Podemos dizer que todas tem módulo . Cada vetor faz um ângulo de com vertical. Então para achar as componentes verticais das forças, a gente faz
Por que a gente usa cosseno? Porque o ângulo está coladinho na vertical, então a gente usa cosseno para achar a componente do vetor nesse eixo.
Passo 4
Agora sim a gente pode usar as equações de equilíbrio. Vamos voltar lá no nosso diagrama
Já vimos que porque todas as forças de compressão têm orientações iguais, todas são iguais
Repara que essas reações ocorrem porque há uma força peso. Essa força está na direção do eixo vertical né? O eixo . E a gente tem a componente de cada forcinha de compressão
Então vamos usar o somatório de forças no eixo . Nesse eixo temos a força peso par abaixo e as componentes de para cima. Como temos 3 forcinhas dessa, nós multiplicamos a componente de uma por 3.
Considerando que as forças positivas estão para cima, nosso somatório fica
Substituindo os dados do problema, lembrando que é a massa do bloco: