Um pião cônico homogêneo de massa tem raio da base e altura (a) Calcule a posição do centro de massa do pião. (b) Com o auxilio do resultado do probl. 5, calcule a velocidade angular de precessão regular do pião quando ele é colocado em rotação rápida, de velocidade angular em torno do seu eixo, com a ponta apoiada no chão. (c) Se o pião precessiona com seu eixo inclinado de em relação a vertical, qual é a força horizontal de reação exercida sobre seu ponto de apoio? (d) Calcule e para , ,
Passo 1
Falaiii galerinha, bora lá?
-
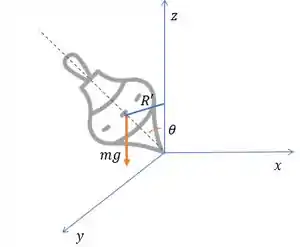
Como o pião é simétrico com relação ao eixo e :
e
No eixo :
Da semelhança . Logo,
Logo,
Como :
Portanto
Passo 2
- A velocidade angular de precessão é
-
Como :
Por fim,
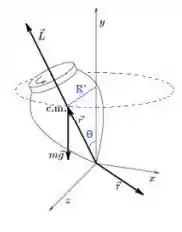
Passo 4
- Substituindo os valores fornecidos, iremos obter como resposta