Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 12.Problemas - Ex. 2

Como aplicação do teorema dos eixos perpendiculares (Probl. 1), calcule: (a) O momento de inércia para uma placa retangular homohenea de massa M e lados a e b em relação a um eixo perpendicular a seu plano, que passsa pelo centro da placa. (b) O momento de inércia de um disco circular de massa M e raio R , em torno de qualquer um seus diâmetros.

Passo 1

(a) Como estamos tratando de uma lamina, podemos usar a densidade superficial, olhá só:

d m = σ d A

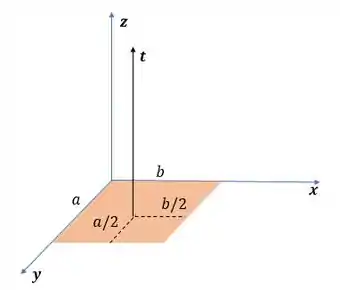
Passo 2

Com relação ao eixo x , temos:

I x = 2 ∫ 0 b / 2 x 2 σ a   d x

Logo,

I x = 2 ⋅ a σ x 3 3 | 0 b 2 = 2 ⋅ a b 3 σ 3 ⋅ 8 = a b 3 σ 12

Como relação ao eixo y é bem parecido!

I y = 2 ⋅ ∫ 0 a / 2 y 2 σ b   d y

Logo,

I x = b σ y 3 3 | 0 a / 2 = 2 ⋅ b a 3 σ 3 ⋅ 8 = b a 3 σ 12

Repara que temos que integrar da metade até o borda por nosso eixo passa pelo centro, e multiplicamos por dois devido ao outro lado da placa.

Como σ = M / a b :

I = I x + I y = a b 3 σ 12 + b a 3 σ 12

Assim,

I = M a b ⋅ a b ⋅ a 2 12 + b 2 12 = M 12 a 2 + b 2

Passo 3

Para a o disco circular o processo é o mesmo!

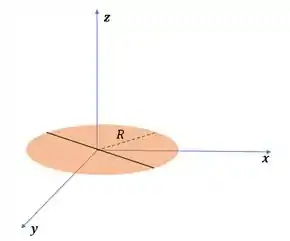
Do problema 1:

I z = I x + I y

Por simetria

I z = 2 I x

I z = ∫ 0 R r 2 d m

Usando que d m = σ d A :

d m = M π R 2 2 π r d r = 2 M R 2 r d r

Logo,

I z = ∫ 0 R r 2 2 M R 2 r d r

Arruamndo as coisas:

I z = 2 M R 2 ⋅ ∫ 0 R r 3 d r = 2 M R 2 ⋅ r 4 4 | 0 R

Finalizando:

I z = M R 2 2

Logo,

I x = M R 2 4

Resposta

  1. I = M 12 a 2 + b 2
  2. I = M R 2 4
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Visando participar de uma equipe de atletas, você e seu amigo Carlos resolver praticar com halteres. Cada um de vocês está usando “A Besta”, um modelo constituído de duas esferas, cada uma de 500 g e
Ao tapear a superfície da água com sua cauda para anunciar perigo, um castor deve girá-la em torno de uma de suas extremidades estreitas. Modelemos a cauda como um retângulo de espessura e massa espec
Use integração para mostrar que o momento de inércia de uma casca esférica fina de raio R e massa m , em relação a um eixo que passa pelo seu centro, vale 2 m R 2 3 .
Para evitar lesionar os ombros, sua idosa avó deseja comprar o batedor de tapetes com o menor momento de inércia em relação à empunhadura. Sabendo que você estuda física, ela solicita seu conselho. Há
Uma vara uniforme, de 2,00 m de comprimento, é elevado a 30 ° com a horizontal em cima de uma camada de gelo. A extremidade de baixo da vara permanece apoiada sobre o gelo. A vara é largada do repouso