Uma haste metálica delgada, de comprimento e massa , pode girar livremente em torno de um eixo horizontal, que a atravessa perpendicularmente, à distância de uma extremidade. A haste é solta a partir do repouso, na posição horizontal. (a) Calcule o momento de inércia da haste, com respeito ao eixo em torno da qual ela gira. (b) Calcule a velocidade angular adquirida pela haste após (Fig.) ter caido de um ângulo , bem como a aceleração .

Vamos ao momento de inércia, mas antes precisamos fazer um desenho.

A nossa ilustração é o seguinte:

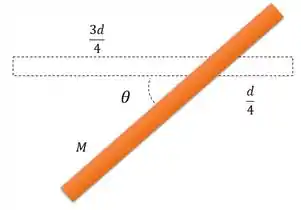
Pra calcular o momento de inércia vamos primeiro fazer o seguinte:

E aí aplicaremos o que foi falado antes:

O momento de inércia de uma barra é:

Para a parte com distância :

Para a parte com distância :

Logo,

Como :

Agora podemos aplicar a conservação da energia, ela vai nos dar uma relação com a velocidade angular.

Inicialmente a barra está parada e só tem energia potencial gravitacional então:

E no final a barra se move com velocidade angular e está a uma outra altura, sendo assim:

Colocando os termos na equação, temos:

Após a barra cair um ângulo :

Rearrumando a velocidade angular :

Como :

E a aceleração angular é:

E pra ficar legalzinho a gente pode passar a variação do tempo pra dentro da raíz: