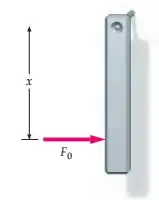
Uma barra uniforme, de massa e comprimento, pende como na figura, livre para girar sem atrito em torno do pivô em uma de suas extremidades. Ela recebe uma pancada horizontal, a uma distância do pivô, como mostrado. (a) Mostre que, imediatamente após a pancada, a rapidez do centro de massa da barra é dada por , onde e são a força média e a duração da pancada, respectivamente. (b) Determine a componente horizontal da força exercida pelo pivô sobre a barra e mostre que esta componente vale zero se . Este ponto (o ponto de impacto para o qual a componente horizontal da força do pivô é zero) é chamado de centro de percussão do sistema barra-pivô.

Vamos achar uma expressão para essa rapidez angular .

Primeiro, a gente pode achar uma expressão para a aceleração angular usando a segunda lei de Newton para a rotação:

Sendo que o torque resultante sobre a nossa barra é causado pela força . E a distância dela até o eixo de rotação é , então o torque resultante vale:

Repara que e são perpendiculares, então o torque é apenas o produto entre eles mesmo. Jogando isso na segunda lei de Newton e isolando a aceleração angular:

Esse é o momento de inércia da nossa barra em relação ao eixo de rotação que está na sua extremidade. Então queremos o momento de inércia de uma barra fina em relação a um eixo que passa pela extremidade dela. Esse tem essa fórmulinha:

Onde é a massa da nossa barra e o comprimento dela. Substituindo isso na nossa expressão da aceleração angular:

Temos então

Mas cara, essa aceleração angular pode ter essa definição:

Esse é o tempo que a força atua mesmo, tá? Esse é o tempo onde teremos aceleração angular, que é causada pelo torque, que é causado pela presença da força. Só que a nossa barra no começo de tudo estava paradinha, então :

Igualando nossas duas expressões de :

Isolando :

Então, jogando essa lá na expressão da rapidez do centro de massa:

b) Para achar a expressão da força que o pivô faz na barra, vamos usar o teorema impulso-quantidade de movimento. Ele diz que:

Só que é a quantidade de movimento que nossa barra ganha (já que ela sai do repouso). A quantidade total de movimento de um sistema pode ser escrita como o produto entre a massa dele e a rapidez do centro de massa. Então para a nossa barra, a gente vai ter:

E o impulso resultante sobre a barra é o impulso com relação a força e com relação a força do pivô. Vamos chamar de o impulso que o pivô faz na barra e o impulso de . Assim:

Aí a equação do teorema fica:

Vamos dar uma incrementada nessa equação. O impulso pode ser escrito como o produto entre a força média e o tempo de ação da força. Então as expressões dos nossos impulsos ficam:

Isso porque a força horizontal do pivô atua enquanto há . Então os tempos de ação delas são iguais. Substituindo na nossa expressão do teorema:

Mas a gente tem a expressão de do item anterior. Vamos substituir aí:

Agora vamos isolar que a gente quer, a força :

Agora vamos descobrir o valor de para que . Só zerar ela na nossa expressão: