Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 3.Problemas - Ex. 32
Um ponto em uma mesa giratória a 20,0 cm do centro acelera do repouso a uma velocidade final de 0,700 m/s em 1,75 s. Em t = 1,25 s, encontre o módulo e a direção da (a) aceleração radial, (b) aceleração tangencial e (c) aceleração total do ponto.
Passo 1
Aqui, migos, pra começar, a gente precisa determinar a aceleração tangencial a partir dos dados do exercício, beleza?
Dados a velocidade final de , a partir do repouso, e o tempo levado pra alcançar essa velocidade, de , a gente consegue achar essa aceleração, mas antes precisamos converter em , a velocidade angular final!
E isso é fácil, pela formulinha que já conhecemos:
No nosso caso, vai valer:
Beleza! Com isso, a gente consegue calcular , a aceleração angular, pela formulinha do vovô ateu pra MCA:
Só aplicar nossos dados que vamos ter:
Legal! Agora a gente vai trabalhar com o vovô ateu pra MCA considerando esse valor de !
Passo 2
Certo. Pra gente responder (a), a aceleração radial ou centrípeta, precisamos usar a clássica formulinha:
Só que a gente quer pra e, pra isso, a gente precisa conhecer a velocidade nesse instante! Como fazer isso?
Justamente a partir do vovô ateu pra MCA. A gente vai começar calculando a velocidade angular no instante e, daí, convertemos em pela formulinha que vamos ver daqui a pouco, mas sei que você já conhece !
Beleza? Considerando (repouso), a aceleração angular calculada no último passo e , vamos aplicar e determinar :
Ok, agora passamos isso pra velocidade linear ou tangencial pela formulinha:
Queremos , então isolamos o termo e aplicamos os dados que temos:
Obtida a velocidade linear, podemos determinar a aceleração radial ou centrípeta! A gente vai ter:
Ah, e quanto a direção dessa aceleração, ela é sempre radial, ou seja, na direção do raio da circunferência, ok? Sempre!
Passo 3
(b)Pra determinar a aceleração tangencial a gente usa uma formulinha análoga a que usamos no último Passo:
Em que (alfa) é a aceleração angular, a aceleração tangencial (ou linear), que queremos calcular aqui, e é o raio.
Ótimo! A gente já conhece o valor de do Passo 1 e também temos o raio. A gente vai ter então:
Essa aceleração, por ser tangencial, tem direção perpendicular ao raio da circunferência, tangenciando a mesma, beleza?!
Passo 4
(c)Então, a aceleração centrípeta e a tangencial que calculamos em (a) e (b) são perpendiculares entre si. Vamos fazer um esqueminha de vetores com elas, e a resultante delas, sem proporção exata, mas considerando os módulos delas:
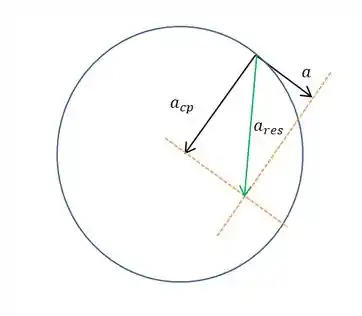
Beleza, gente, a aceleração resultante, ou total, tem então essa direção, secante à circunferência, certo? Mas e o módulo?
Basta a gente aplicar Pitágoras, sendo o módulo da resultante a nossa hipotenusa, beleza? A gente vai ter:
Resposta
(a)
(b)
(c)