Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.2 - Ex. 29
Uma porta tem uma altura de , ao longo de um eixo que se estende verticalmente para cima, e uma largura de , ao longo de um eixo que se estende horizontalmente a partir do lado da porta que está preso com dobradiças. Uma das dobradiças está a da borda superior da porta e outra a da borda inferior; cada uma sustenta metade do peso da porta, cuja massa é . Em termos dos vetores unitários, qual é a força exercida sobre
a porta (a) pela dobradiça superior e (b) pela dobradiça inferior?
Passo 1
Fala galerinha bonita, tudo beleza?
Saca só, nesse exercício aqui, primeiro a gente pode desenhar o diagrama de corpo livre para a porta.
Olha só como fica o diagrama das forças que atuam sobre a porta como um todo:
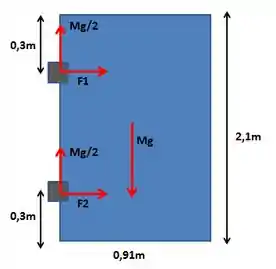
A questão já nos dá duas informações importantes: “As duas dobradiças suportam metade do peso da porta”. Por isso, no diagrama da figura acima elas exercem forças iguais a sobre a porta, verticalmente para cima. Considerando como e as forças que elas exercem horizontalmente, vamos seguir para os próximos passos.
Passo 2
Lembra lá do equilíbrio de torques? Como a porta em questão está em equilíbrio, podemos usá-lo para responder o problema. Considerando o equilíbrio de torques com relação à dobradiça de baixo, temos:
Nessa equação, a gente consegue isolar e obter a resposta da letra (a):
Passo 3
Não acabou ainda! Para terminar, vamos escrever a força exercida pela dobradiça superior na notação de vetores unitários, lembrando que o módulo de sua componente horizontal é igual ao de e o da sua componente vertical é igual a metade do peso da porta:
Então, temos que:
Passo 4
(b) Para encontrar , um caminho possível é usar o equilíbrio de forças na horizontal:
Agora, para encontrarmos a força da dobradiça inferior vetorialmente, temos:
Resposta
(a)
(b)