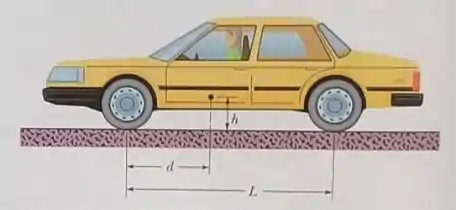
Na figura, a motorista de um carro que se move em uma estrada horizontal faz uma parada de emergÊncia aplicando os freios de tal forma que as quatro rodas ficam bloqueadas e derrapam na pista. O coeficiente de atrito cinético entre os pneus e a pista é A distância entre os eixos dianteiro e traseiro é e o centro de massa do carro está a uma distância atrás do eixo dianteiro e a uma altura acima da pista. O carro pesa Determine o módulo (a)da aceleração do carro durante a frenagem. (b da força normal a que uma das rodas traseiras é submetida, (c) da força noral a que uma das rodas dianteiras é submetida, (d)da força de frenagem a que uma das rodas traseiras é submetida, e (e)da força de frenagem a que uma das rodas dianteiras é submetida. (Sugestão: Embora o carro não esteja em equilíbrio para translações, está em equilíbro para rotações.)

(b)Considere as forças aplicadas sobre o carro, demonstradas na figura abaixo:

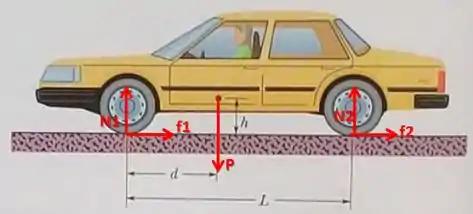
Analisando o equilíbrio de torques com relação ao centro de massa, temos:

Então:

Substituindo na equação acima, temos:

Ou seja:

Atenção! Essa força representa a soma das forças que agem sobre as duas rodas traseiras. Para encontrar a força que age em cada roda temos que dividir esse resultado por 2:

(c)Aqui, nos é pedido o valor de . Para encontrá-lo, é só usarmos o valor de que encontramos acima, já que:

Então:

Lembrando que representa a soma das forças que agem sobre as duas rodas dianteiras. Assim,temos:

(d)Para encontrar a força de atrito sobre cada roda traseira, é só multiplicar a força normal encontrada no passo 2 pelo coeficiente de atrito:

(e)Do mesmo modo, temos que multiplicar aqui o coeficiente de atrito pela força normal encontrada no passo 3: