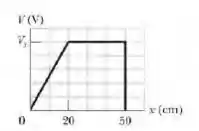
Um pósitron (carga , massa igual à do elétron) está se movendo com uma velocidade de no sentido positivo do eixo quando, em , encontra um campo elétrico paralelo ao eixo . A Fig. abaixo mostra o potencial elétrico associado ao campo. A escala do eixo vertical é definida por . (a) O pósitron emerge da região em que existe campo em (o que significa que o movimento se inverte) ou em (o que significa que o movimento não se inverte)? (b) Com que velocidade o pósitron emerge da região?

Podemos usar a relação , em que é o potencial elétrico de uma carga, é a carga e é o potencial dela para alterar a informação que temos do gráfico que é de potencial para potencial elétrico. Portanto, de acordo com o enunciado, a energia cinética inicial, em elétron-volts é:

Como é menor do que a barreira que vemos do gráfico de , então o pósitron tem o seu movimento invertido quando entra na região de campo elétrico, então, ele emerge do campo elétrico no ponto .

Tranquilo até aqui? 👀

Bem, de acordo com a lei de conservação da energia, como o potencial inicial e final são iguais a zero (como no gráfico), as velocidades inicial e final tem que ser iguais. Portanto, a velocidade final é

Fim! Iae, o que achou? Responde Aí! 😁