Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.7 - Ex. 34

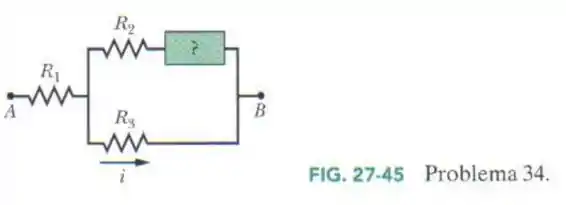
A Fig. 27-45 mostra uma parte de um circuito. As resistências são R 1 = 2,0 Ω , R 2 = 4,0 Ω e R 3 = 6,0 Ω e a corrente indicada é i = 6,0 A . A diferença de potencial entre os pontos A e B que ligam o conjunto ao resto do circuito é V A - V B = 78 V . (a) O elemento representado como "?" está absorvendo energia do circuito ou cedendo energia ao circuito? (b) Qual é a potência absorvida ou fornecida pelo elemento desconhecido?

Passo 1

Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Aqui temos uma situação onde um elemento misterioso pode estar absorvendo energia ao circuito ou pode estar cedendo energia para o circuito.

Passo 2

Podemos calcular a ddp em cima da resistência 3:

V 3 = i R 3

V 3 = 6,0 6,0 = 36 V

Dessa forma, podemos calcular a diferença de potência em cima da resistência 1, pois:

V A – V B = V 1 + V 3

→ V 1 = V A – V B - V 3

V 1 = 78 - 36 = 42 V

A corrente que passa pelo resistor 1 é:

i 1 = V 1 R 1

i 1 = 42 2,0 = 21   A

Portanto, a corrente no resistor 2 é:

i 2 = i 1 - i

i 2 = 21 - 6,0 = 15 A

Passo 3

Assim, a potência dissipada no circuito é a corrente dissipada em cada resistor.

P = P 1 + P 2 + P 3

P = i 1 2 R 1 + i 2 2 R 2 + i 2 R 3

P = 21 2 2,0 + 15 2 4,0 + 6,0 2 6,0 = 1998 W

Essa é a potência que está sendo dissipada no circuito, porém desconsiderando o elemento “?”, temos que a potência é:

P ' = i 1 V A B

P ' = 21 78 = 1638 W

Ou seja, o elemento “?” está colocando energia no sistema.

Passo 4

(b) Para calcular a potência fornecida pelo elemento:

P - P ' = 1998 - 1638 = 360 W

Resposta

(a) Colocando energia

(b) P ? = 360 W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nove fios de cobre de comprimento l e diâmetro d estão ligados em paralelo formando um único condutor composto de resistência R. Qual deverá ser o diâmetro D de um único fio de cobre de comprimento I,
Dispõe-se de duas baterias de fem E e resistência interna r. Elas podem ser ligadas em paralelo (Fig. 29-29a) ou em série (Fig. 29-29b) e são usadas para estabelecer uma corrente num resistor R. (a) O
A Fig. 29-11a mostra 12 resistores, cada um de resistência R, formando um cubo. (a) Determine Req, a resistência equivalente entre as extremidades da diagonal de uma face. (b) Determine R17, a resistê
(a) Calcule a corrente que atravessa cada uma das baterias ideais da Fig. 29-31. Suponha que R1 = 1,0 Ω, R2 = 2,0 Ω, E1 = 2,0 V e E2 = E3 = 4,0 V. (b) Calcule Va- Vb.
(a) Na Fig. 29-32, qual é a resistência equivalente do circuito elétrico mostrado? (b) Qual é a corrente em cada resistor? Faça R1 = 100 Ω, R2=R3=50 Ω , R4 =75 Ω e E=6.0 V; suponha que a bateria é ide