Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 20
Uma prancha de , com de massa, é articulada em uma de suas extremidades. Uma força é aplicada verticalmente sobre a outra extremidade, e a prancha forma um ângulo de com a horizontal. Um bloco de é colocado sobre a prancha, a da articulação, como mostrado na Figura 12-34. (a) Determine a magnitude da força . (b) Determine a força exercida pela articulação. (c) Determine a magnitude da força , bem como a força exercida pela articulação, se for exercida, agora, formando um ângulo reto com a prancha.
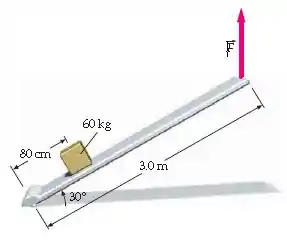
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O diagrama de corpo livre do sistema é dado por:
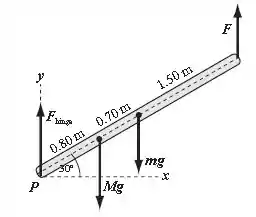
Aplicando , temos:
Substituindo os valores, temos:
Passo 2
Item (b):
A força exercida pela articulação pode ser obtida através da aplicação da segunda lei de Newton. Temos:
Substituindo os valores, temos:
Passo 3
Item (c):
O novo diagrama para o sistema está exposto abaixo:
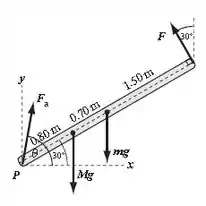
Aplicando , temos:
Substituindo os valores, temos:
A força exercida pela articulação pode ser obtida através da aplicação da segunda lei de Newton. Temos:
Dividindo as equações, temos:
Substituindo os valores, temos:
Portanto: