Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 12.Problemas - Ex. 11

Prende-se ao teta a ponta de uma fita métrica leve, enrolada num estojo circular de massa m e raio r , e solta-se o estojo em repouso (Fig.). (a) Calcule a aceleração linear do estojo. (b) Calcule a tensão da fita. (c) Calcule a velocidade linear do estojo depois que um comprimento s da fita se desenrolou. Verifique a conservação da energia.

Passo 1

Se liga nessa ilustração:

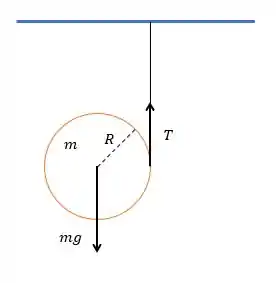
(a) Como queremos saber a aceleração linear do estojo, vamos escrever as equações de Newton.

m g - T = m a     ( i )

Além disso, podemos calcular o torque com relação ao centro do estojo.

τ r e s = I α

Logo,

T ⋅ r = I α

Como a = α r e I = m r 2 2 :

T ⋅ r = m r 2 2 ⋅ a r     ( i i )

Isolando a tração em ( i ) e substituindo em ( i i ) :

m g - m a ⋅ r = m r 2 2 ⋅ a r  

Arrumando as coisas, temos:

2 ⋅ g - a = a → a = 2 3 g

Passo 2

(b) Para calcular a tração, podemos usar a equação ( i ) .

m g - T = m a

Como a = 2 3 g :

m g - T = m ⋅ 2 3 g

Logo,

T = m g 3

Passo 3

(c) Por fim, podemos conservar energia para achar a velocidade.

Δ E c = W t

Logo,

I ω 2 2 + m v 2 2 = m g s

Como ω = v / r e I = m r 2 2 :

m r 2 2 ⋅ v r 2 2 + m v 2 2 = m g s

Isolando o termo v 2 :

v 2 4 + v 2 2 = g s

Logo,

v 2 = 4 g s 3

Para verificar a conservação da energia, podemos utilizar o valor da aceleração calculado no item (a) para achar a velocidade.

Da cinemática, temos:

v 2 = v 0 2 + 2 a Δ s

Como velocidade inical é nula:

v 2 = 2 a s → v 2 = 2 ⋅ 2 3 g ⋅ s = 4 g s 3

Logo, a energia se conservou!

Resposta

  1. a = 2 3 g
  2. T = m g 3
  3. v = 4 g s 3
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Objeto cilíndrico não homogêneo. Na figura abaixo um objeto cilíndrico de massa M e raio R rola suavemente descendo uma rampa, a partir do repouso, e passa por um trecho horizontal de pista. Em seguid
Em 1980 , sobre a baía de São Francisco, um grande ioiô foi solto de um guindaste. O ioiô de 116 k g era formado por dois discos homogêneos com 32 c m de raio, ligados por um eixo com 3,2 c m de raio.
Um ioiô possui um momento de inércia de 950 g c m ² ² e uma massa de 120 g . O raio do eixo é 3,2 m m e a corda tem 120 c m de comprimento. O ioiô rola para baixo, a partir do repouso, até a extremida
Um mecanismo em forma de ioiô, montado em um eixo horizontal sem atrito, é usado para levantar uma caixa de 30kg , como mostra a figura abaixo. O raio externo R da roda é 0,5m e o raio r do cubo da ro
Na figura abaixo, quatro polias estão ligadas por duas correias. A polia A (de 15 c m de raio) é a polia motriz e gira a 10 r a d / s . A polia B ( 10 c m de raio) está ligada à polia A pela correia 1