Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.4 - Ex. 16

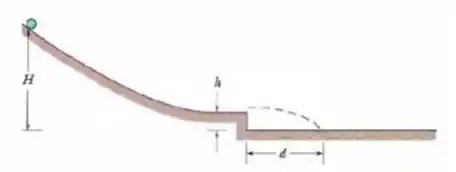
Objeto cilíndrico não homogêneo. Na figura abaixo um objeto cilíndrico de massa M e raio R rola suavemente descendo uma rampa, a partir do repouso, e passa por um trecho horizontal de pista. Em seguida, rola para fora da pista, pousando a uma distância horizontal d = 0,506 m do final da pista. A altura inicial do objeto é H = 0,9 m ; a extremidade da pista está a uma altura de h = 0,10 m . O objeto é composto por uma camada cilíndrica central, também homogêneo (com massa específica) e um cilindro central, também homogêneo ( com uma massa específica diferente). O momento de inércia do objeto é dado pela expressão geral I = β M R 2 , mas β não é igual a 0,5 , como no caso de um cilindro homogêneo. Determine o valor de β .

Passo 1

Olá pessoal, tudo bem? Vamos praticar um pouco?

Bom, como no sistema não há perda de energia, então podemos usar o princípio da conservação de energia no ponto mais alto, de altura H e na parte horizontal.

Na parte superior temos apenas a energia potencial gravitacional, pois o objeto parte do repouso. Na pista horizontal vamos ter a energia potencial gravitacional mais a energia cinética (de rotação e de translação). O valor das energias é o mesmo nesses dois pontos, então:

M g H = M g h + I ω 2 2 + M v 2 2

Nossa missão agora é encontrar a velocidade. Para isso vamos olhar para o movimento que acontece depois que o cilindro deixa a plataforma.

Passo 2

O alcance da bola foi de d = 0,506 m e podemos relacionar o tempo de queda com o deslocamento horizontal. Sabendo que o cilindro apenas tinha velocidade horizontal podemos calcular a velocidade dele. Mas pra isso precisamos do tempo! Vamos olhar o movimento na vertical então.

Da cinemática sabemos que o tempo de queda de um objeto em queda livre partindo do repouso é:

h = g t 2 2

Ou seja,

t = 2 h / g

No nosso caso h = 0,1 m . Assim o tempo de queda foi:

t = 2.0,1 9,8 = 0,14 s

Agora da cinemática horizontal, podemos calcular a velocidade:

v = d t = 0,506 0,14 = 3,61   m / s

Agora sim vamos voltar lá pra equação do passo 1 !

Passo 3

A expressão do passo 1 que achamos foi:

M g H = M g h + I ω 2 2 + M v 2 2

Sabendo que o cilindro rola sem deslizar, a relação v = ω r é válida!

Substituindo os valores de v , H , h , g ,   I = β M R 2 e ω = v / R temos:

9,8.0,9 M = 9,8.0,1 . M + 1 2 β M R 2 . 3,61 R 2 + M 3,61 2 2

Podemos cortar M em todos os termos e simplificando R 2 no segundo termo do lado direito ficamos com:

8,82 = 0,98 + 6,51 β + 6,51

6,51 β = 1,33

β = 0,204

Feito!

Vamos pra próxima?

Resposta

β = 0,204

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12.32. O objeto da figura ex12.32 se encontra em equilíbrio? Explique.
33 . || Os dois objetos da F I G U R AE X 12.33 equilibram-se sobre um pivô. Quanto vale a distância d ?
Um fio fino e leve está enrolado na borda externa de um cilindro oco uniforme com massa de 4,75 kg, tendo os raios interno e externo conforme mostra a Figura abaixo. O cilindro é liberado do repouso.
9.15Q Um paradoxo: quando a haste vista na Figura 10.43 cai sem mover o pé de apoio, seu centro de massa se desloca se desloca para direita, o que significa que, devido ao atrito, a mesa exerce uma fo
9.14P Ainda com referência à haste em queda na Figura 9.20, supondo que seu ponto de apoio fique imóvel, calcule a aceleração angular em função do ângulo θ .