Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.Problemas Adicionais - Ex. 111
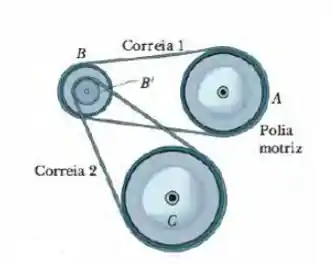
Na figura abaixo, quatro polias estão ligadas por duas correias. A polia (de de raio) é a polia motriz e gira a . A polia ( de raio) está ligada à polia pela correia . A polia ( de raio) é concêntrica com a polia e está rigidamente ligada a ela. A polia (de de raio) está ligada à polia pela correia . Calcule:
a velocidade linear de um ponto da correia ,
a velocidade angular da polia ,
a velocidade angular da polia , a
a velocidade linear de um ponto da correia e
a velocidade angular da polia .
Sugestão: se a correia entre duas polias não desliza, as velocidades lineares das bordas das duas polias são iguais.
Passo 1
Falaa aii galerinha bonita, tudo belejóia?!! Vamos praticar o cálculo de rotações? Partiuu!!
A correia está ligada na polia motriz, a velocidade linear vai ser dada pela multiplicação da velocidade angular e o raio de :
Dessa forma, susbituindo os valores que o enunciado nos fornece, descobrimos que:
Passo 2
Agora para a polia , a velocidade será dada como:
Mas como a gente é malandro, vamos seguir a sugestão do problema!!
Como a polia tá ligada pela mesma correia que a polia , as velocidades lineares serão iguais. E daí podemos tirar a velocidade angular de :
Tal que:
Passo 3
E a polia ?
Bom, ela não está acoplada e rigidamente ligada a polia ? Então elas giram juntinhas! Assim, a velocidade angular da polia é exatamente igual a velocidade angular da polia que acabamos de encontrar!
Passo 4
A velocidade linear da correia pode ser determinada a partir do valor velocidade angular da polia . Como podemos relacionar a velocidade angular e a linear pela fórmula “quem-vê-bunda-ri”:
Passo 5
Agora queremos saber a velocidade angular da polia . Bom, já estamos carecas de saber que polias ligadas a mesma correia possuem a mesma velocidade linear, não é mesmo? Então a velocidade linear da polia é a mesma velocidade linear da polia .
Maaas o que queremos é a velocidade angular, tal que:
