Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 16.1 - Ex. 85
Em princípio, uma onda com praticamente qualquer forma arbitrária pode ser expressa como uma soma de ondas harmônicas de diferentes frequências. (a) Considere a função definida por
Escreva um programa de planilha eletrônica para calcular esta série usando um número finito de termos, e faça três gráficos da função, na faixa de a . Para criar o primeiro gráfico, aproxime a soma de até pelo primeiro termo da soma, para cada valor de que você plotar. Para criar os segundo e terceiro gráficos, use apenas os cinco primeiros termos e os dez primeiros termos, respectivamente. Esta função é, às vezes, chamada de função quadrada. (b) Diga qual é a relação entre esta função e a série de Leibnitz para ,
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
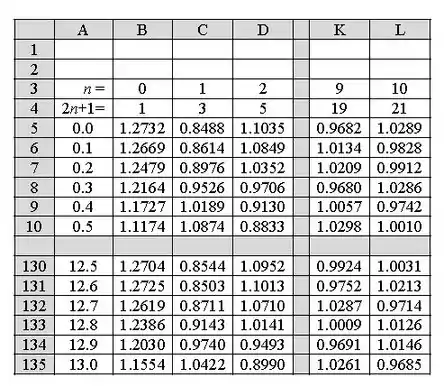
Um esboço dos dados inseridos na planilha está exposto abaixo:
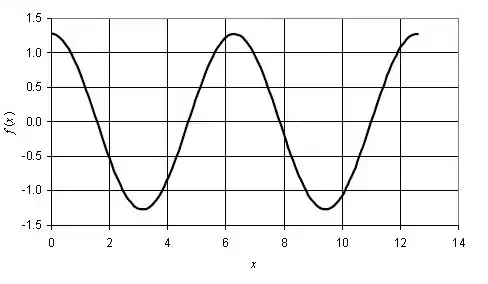
O gráfico de versus , para , deve ficar desta maneira:
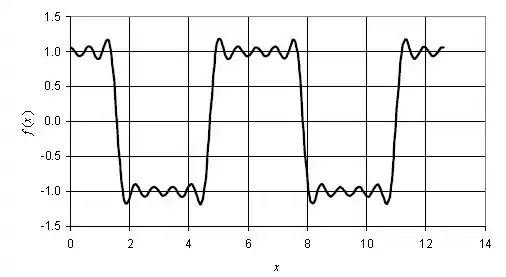
O gráfico de versus , para , deve ficar desta maneira:
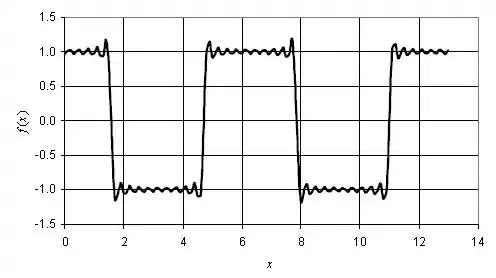
O gráfico de versus , para , deve ficar desta maneira:
Temos que:
Esta sequencia converge para :
Que é equivalente a fórmula de Liebnitz.
Resposta
Ei, a resposta está no passo a passo :)