Potência instantânea em uma onda estacionária. De acordo com a Equação (15.21), a taxa instantânea de energia transferida por uma onda ao longo de uma corda ( a potência instantânea) é dada por
Onde é a tensão.
a) Obtenha para uma onda estacionária dada pela Equação (15.28).
b) Mostre que para todos os valores de a potência média transportada pela onda é igual a zero. (A Equação 15.25) não se aplica para ete caso. Você pode explicar por quê?)
c) Para uma onda estacionária dada pela Equação (15.28), faça um gráfico de e do deslocamento em função de para , , e . (Um valor positivo de indica que a energia flui no sentido crescente , um valor negativo de indica que a energia flui no sentido decrescente .)
d) A energia cinética por unidade de comprimento da corda é mais elevada nos locais onde a corda possui maior velocidade transversal e a energia potencial por unidade de comprimento da corda é mais elevada nos locais onde a corda possui maior inclinação (porque neste ponto ocorre maior tensão na corda). (Vjea o problema desafiador 15.81). Usando essas ideias, discuta a transfencia de energia ao longo da corda.
Passo 1
A função de onda que quermos começar analisando é a seguinte:
A equação que vamos utilizar para calcular a potência é:
Passo 2
a) Para calcular a potencia da nossa função de onda precisamos calcular a primeira derivada no tempo e no espaço.
Derivada no tempo:
Derivada no espaço:
Substituindo na equação da potência:
Passo 3
b) O valor médio da potência é proporcional a e se calcularmos a média de uma função seno iremos verificar que é zero, logo a portência média é igual a zero.
Para a equação isso não se aplica, pois nela não tem nenhuma função seno logo o valor da potência média será diferente de zero.
Passo 4
c) Para plotar o gráfico vamos utilizar a equação da potência que obtemos no item (a).
Gráfico de :
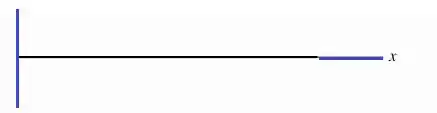
Gráfico de :
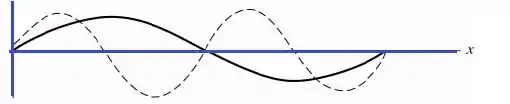
Gráfico de :

Gráfico de :
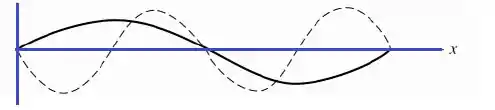
Passo 5
d) Quando a corda estacionária está em seu deslocamento máximo em todos os pontos, toda a energia é potencial e é concentrada nos locais onde a inclinação é mais ingrime (os nós). Quando a onda estacionária tem deslocamento zero toda a energia é cinética e fica concentrada onde as partículas se movem mais rapidamente (os antinodos). Então a energia deve ser transferidas dos nós para o antinodos e vice-versa. Observe que P é maior entre os nós e antinodos adjacentes, é que P desaparece nos nós e antinodos.
Resposta
Ei, a resposta está no passo a passo :)