Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 127

Em problemas envolvendo uma polia com momento de inércia não-nulo, as magnitudes das tensões da corda, nos dois lados da polia, são diferentes. A diferença de tensão é devida à força de atrito estático entre a corda e a polia; no entanto, a força de atrito estático não pode ser arbitrariamente grande. Considere uma corda sem massa envolvendo parcialmente um cilindro, de um ângulo Δ θ (medido em radianos). Pode ser mostrado que, se a tensão em um lado da polia é T , enquanto que a tensão no outro lado é T ' ( T ' > T ), o maior valor de T ' que pode ser mantido sem que a corda deslize é T m a x ' = T e μ e Δ θ , onde μ c é o coeficiente de atrito estático. Seja a máquina de Atwood da figura: a polia tem raio R = 0.15 m , momento de inércia I = 0.35   k g ⋅ m 2 e o coeficiente de atrito estático entre a polia e o cordão é μ c = 0.30 . (a) Se a tensão em um dos lados da polia é 10 N , qual é a máxima tensão do outro lado para a qual a corda não desliza sobre a polia? (b) Qual é a aceleração dos blocos, neste caso? (c) Se a massa de um dos blocos pendurados é 1,0 k g , qual é a maior massa que pode ter o outro bloco se, após liberados, a polia gira sem ocorrer deslizamento?

Passo 1

Pra começar uma questão de dinâmica, a melhor coisa é desenhar o diagrama de corpo livre.

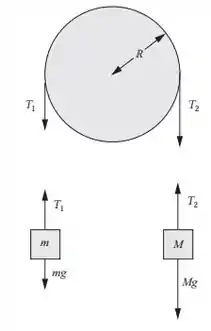
Passo 2

  1. Com a fórmula que ele deu no enunciado fica mole achar a tensão máxima:

    2. T m a x ' = T e μ c Δ θ

    Como a corda envolve metade do cilindro, Δ θ = π .

    T m a x ' = 10 N e 0.30 π

    T m a x ' = 25.66 N

    T m a x ' ≅ 26 N

    Passo 3

  2. Relacionando T 2 e T 1 :

    3. T 2 = T 1 e 0.30 π

    Da condição de que a corda não estica, sabemos que a = α R . Usando a segunda lei de Newton para a polia:

    ∑ τ = T 2 - T 1 R = I α

    T 1 e 0.30 π - T 1 R = I a R

    T 1 = I a e 0.30 π - 1 R 2

    Para o bloco de massa m :

    T 1 - m g = m a → T 1 = m a + m g

    Juntando as duas e arrumando a casa:

    I a e 0.30 π - 1 R 2 = m a + m g

    a = g I e 0.30 π - 1 m R 2 - 1

    Substituindo os valores numéricos:

    a = 9.81 I e 0.30 π - 1 1 × 0.15 2 - 1

    Com o auxílio da calculadora a gente obtém:

    a = 1.098   m / s 2

    Passo 4

  3. Para o bloco de massa M :

M g - T 2 = M a

M = T 2 g - a

Como T 2 = T 1 e 0.30 π , e T 1 = m ( a + g ) :

M = m a + g e 0.30 π g - a

Substituindo valores:

M = 1.0 1.098 + 9.81 e 0.30 π 9.81 - 1.098

M = 3.2 k g

Resposta

  1. T m a x ' ≅ 26 N
  2. a = 1.098   m / s 2
  3. M = 3.2 k g
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12.32. O objeto da figura ex12.32 se encontra em equilíbrio? Explique.
33 . || Os dois objetos da F I G U R AE X 12.33 equilibram-se sobre um pivô. Quanto vale a distância d ?
Um fio fino e leve está enrolado na borda externa de um cilindro oco uniforme com massa de 4,75 kg, tendo os raios interno e externo conforme mostra a Figura abaixo. O cilindro é liberado do repouso.
9.15Q Um paradoxo: quando a haste vista na Figura 10.43 cai sem mover o pé de apoio, seu centro de massa se desloca se desloca para direita, o que significa que, devido ao atrito, a mesa exerce uma fo
9.14P Ainda com referência à haste em queda na Figura 9.20, supondo que seu ponto de apoio fique imóvel, calcule a aceleração angular em função do ângulo θ .