Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 32
12.32. O objeto da figura ex12.32 se encontra em equilíbrio? Explique.
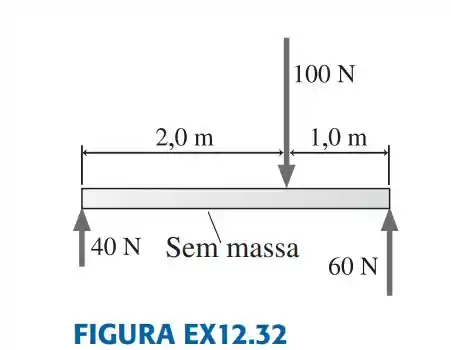
Passo 1
Bom, para o objeto estar em equilíbrio ele tem que satisfazer duas condições: A força resultante tem que ser e o torque no centro de massa do objeto também tem que ser .
Bom, vamos começar pela primeira condição
Todas as forças tem mesma direção. Vamos assumir para cima como sentido positivo
Então a primeira condição está satisfeita, a força resultante é . Esse resultado significa que o objeto não translada.
Passo 2
Agora vamos para a segunda condição. Bom, se o torque no objeto for nulo, quando a gente calcular o torque no ponto em que aplicamos a força de , o torque tem que ser , assim as forças se igualam e o objeto não rotaciona. Vamos calcular o torque nesse ponto. Começando pela força de .
Agora vamos calcular para a outra força
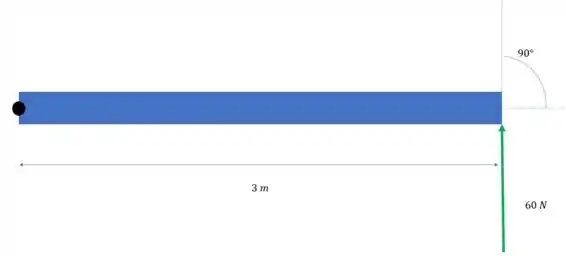
Agora vamos calcular o torque total e
Bom, o resultado necessário para que o a barra não rotacione é , como não obtivemos isso, podemos concluir que o objeto não está em equilíbrio, ele está rodando.
Resposta
Não está em equilíbrio.