Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 10.Problemas - Ex. 25
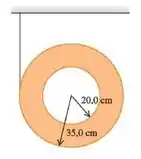
Um fio fino e leve está enrolado na borda externa de um cilindro oco uniforme com massa de kg, tendo os raios interno e externo conforme mostra a Figura abaixo. O cilindro é liberado do repouso. (a) Até que distância o cilindro deverá cair antes que seu centro esteja se movendo a m/s? (b) Se você simplesmente soltasse esse cilindro sem qualquer fio, com que velocidade seu centro estaria se movendo quando tivesse caído a uma distância igual à da parte (a)? (c) Por que existem duas respostas diferentes, se o cilindro cai pela mesma distância nos dois casos?
Passo 1
Tudo tranquilo? Vamos analisar o item (a). Nele precisaremos saber até que distância que o cilindro deve cair para que a velocidade de seu centro não seja m/s. Como sabemos, a energia cinética inicial do cilindro é e a final ( é dada pela seguinte equação:
Onde o momento de inércia , em relação ao eixo de simetria, é:
Onde, é o raio interno e o raio externo. A velocidade angular, devido ao fio estar conectado à parte externa do cilindro, é:
Portanto, , para o cilindro mostrado na figura, é:
Agora iremos achar o valor da distância percorrida pelo cilindro utilizando a lei da conservação de energia, sabendo que as energias potenciais são e . Veja!
Substituindo os valores, temos:
Passo 2
Item (b). Como o valor a distância percorrida é , caso não tivéssemos o fio, o valor da velocidade no centro do cilindro seria dado por:
Passo 3
Item (c). Do ponto de vista da energia, o fio é simplesmente um meio de converter parte da energia potencial gravitacional (liberada quando o cilindro cai) em energia cinética de rotação, em vez de energia cinética de translação. Como nem toda a energia liberada vai para a translação, é menor que ., que é a velocidade que um objeto atinge ao cair de uma altura sem qualquer fio preso.
Resposta
(A) Passo
(B) Passo
(C) Passo