Um projétil é disparado a acima da horizontal. Quaisquer efeitos devidos à resistência do ar são desprezíveis. A velocidade inicial do projétil no problema tem um componente vertical que é (a) menor que , (b) maior do que , (c) igual a , (d) não pode ser determinada a partir das informações dadas.
Passo 1
Vamos desenhar o vetor da velocidade no instante em que o projétil é disparado:
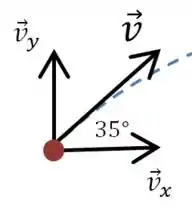
Sabemos pelas informações do problema que a componente horizontal da velocidade inicial é:
Então podemos escrever as seguintes expressões para as componentes e :
Passo 2
E já podemos calcular o módulo da componente vertical da velocidade inicial:
Então a resposta certa é a letra (a).
Na verdade nem precisaríamos fazer a conta, bastava lembrar que para qualquer ângulo abaixo de , e como nosso ângulo é de , necessariamente teríamos .
Resposta
Letra (a).