Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 21.Exercícios - Ex. 77

Um próton é projetado para o interior de um campo elétrico uniforme que aponta verticalmente para cima e possui módulo E. A velocidade inicial do próton possui módulo v 0 e sua direção forma um ângulo α com a horizontal. (a) Calcule a distância máxima h m á x que o próton desce verticalmente abaixo de sua altura inicial. Despreze as forças gravitacionais. (b) Depois de qual distância horizontal d o próton retorna a sua altura inicial? (c) Faça um esboço da trajetória do próton. (d) Calcule os valores numéricos de h m á x e d , sabendo que E = 500   N / C , v 0 = 4,0 × 10 5   m / s e α = 30,0 ° .

Passo 1

Temos o seguinte esquema. Note que desenhamos as orientações dos eixos x e y .

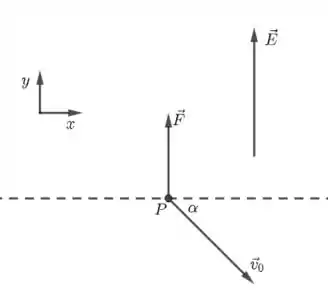
A força F → é a força elétrica, cujo módulo é dado por

F = q E

sendo q a carga do próton. Para estudarmos o movimento, vamos dividi-lo no eixo x e y .

Passo 2

No eixo x não há nenhuma força. Assim, a velocidade em x é mantida constante e vale

v x = v 0 cos ⁡ α

Assim, temos um movimento uniforme, de modo que podemos escrever a posição x em função do tempo t :

x = v 0 cos ⁡ α t

Passo 3

No eixo y há apenas a força elétrica (estamos desprezando o peso, já que a massa do próton é muito pequena). Assim, temos

F y = E q

Usando a 2° lei de Newton:

m a y = E q ∴ a y = E q m

Note que tem um movimento uniformemente acelerado no eixo y . Assim, temos

y = v 0 y t + 1 2 a y t 2 = - v 0 sin ⁡ α t + 1 2 E q m t 2

note que tomamos a velocidade negativa pois ela está para baixo.

Também podemos expressar a velocidade no eixo y em função do tempo:

v y = v 0 y + a y t ⟹ v y = - v 0 sin ⁡ α + E q m t

Por fim, podemos escrever a equação de Torricelli para o eixo y :

v y 2 = - v 0 sin ⁡ α 2 + 2 a y Δ y = v 0 2 sin 2 ⁡ α + 2 E q m Δ y

Passo 4

(a) Enquanto a velocidade v y for negativa (ou seja, apontar para baixo) o próton irá continuar descendo. Observe ainda que a aceleração a y faz o próton incialmente desacelerar até que v y = 0 . Nesse instante obtemos a altura máxima. Assim, na equação de Torricelli pra o eixo y :

0 = v 0 2 sin 2 ⁡ α + 2 E q m h m á x ⟹ h m á x = - m v 0 2 sin 2 ⁡ α 2 E q

Encontramos h m á x < 0 , já que tal posição está abaixo do eixo x .

Passo 5

(b) Vamos calcular o tempo t que o próton demora para retomar a y = 0 . Para fazer isso, basta colocarmos y = 0 na equação:

0 = - v 0 sin ⁡ α t + 1 2 E q m t 2 ∴ t E q 2 m t - v 0 sin ⁡ α = 0

Note que temos duas raízes. A primeira t = 0 não nos interessa; a segunda é:

t = 2 m v 0 sin ⁡ α E q

Substituindo o valor de t na equação de x versus t , temos:

x = v 0 cos ⁡ α t ⟹ d = v 0 cos ⁡ α 2 m v 0 sin ⁡ α E q ∴ d = m E q v 0 2 sin ⁡ 2 α

onde usamos a relação 2 sin ⁡ α cos ⁡ α = sin ⁡ 2 α .

Passo 6

Podemos obter analiticamente a equação da trajetória isolando t na equação x versus t :

x = v 0   cos ⁡ α t ∴ t = x v 0 cos ⁡ α

Assim, colocando na equação de y versus t :

y = - v 0 sin ⁡ α ⋅ x v 0 cos ⁡ α + 1 2 E q m x v 0 cos ⁡ α 2

y = - tan ⁡ α x + E q 2 m v 0 2 cos 2 ⁡ α x 2

Note que temos a equação de uma parábola com concavidade voltada para cima. Temos o seguinte esboço.

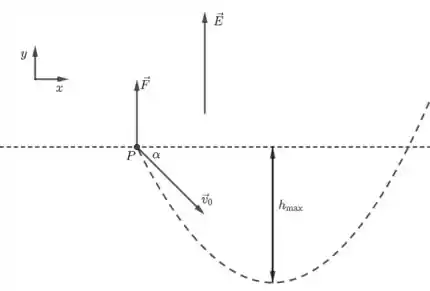
Passo 7

O enunciado não nos forneceu a massa do próton e nem sua carga. Podemos obter tal valor através de uma tabela ou procurando na internet. Os valores tabelados são m = 1,67 × 10 - 27   k g e q = 1,6 × 10 - 19 C . Logo:

h m á x = - m v 0 2 sin 2 ⁡ α 2 E q = - 1,67 × 10 - 27   k g 4,0 × 10 5   m ⋅ s - 1 2 sin ⁡ 30 ° 2 2 500   N ⋅ C - 1 1,6 × 10 - 19   C = - 0,418   m

d = m E q v 0 2 sin ⁡ 2 α = 1,67 × 10 - 27 k g 4,0 × 10 5   m ⋅ s - 1 2   sin ⁡ 60 ° 2 500   N ⋅ C - 1 1,6 × 10 - 19   C = 2,89   m

Resposta

  1. h m á x = - m v 0 2 sin 2 ��� α 2 E q .
  2. d = m E q v 0 2 sin ⁡ 2 α .
  3. Ver esquema.
  4. h m á x = - 0,418   m e d = 2,89   m .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas partículas cujas cargas são q 1=0,500n Ceq 2=8,0n C estão separadas por uma distância de 1,2m . Em que o ponto entre as cargas e o campo elétrico resultante das duas cargas é igual a zero?
Uma carga puntiforme q 1=-4,0n C está no ponto x=0,600m ,y=0,8m ; e outra carga puntiforme q 2=+6,0n C está no ponto x=0,600m ,y=0 . Calcule o módulo, direção e o sentido do campo elétrico na origem p
A distância entre dois planos carregados infinitos é igual a d . O plano inferior carregado negativamente possui uma densidade superficial de carga - σ0 . O plano superior carregado positivamente poss
Uma carga puntiforme positiva q colocada no ponto x=a outra carga puntiforme negativa - q é colocada no ponto x=-a .Determine o módulo, a direção e o sentido do campo elétrico no ponto x=0 . Expressão
Repita o exercício 21. 44, considerando que q 1 = - 4,0n C . Dados: q 1=- 4,0n C q 2=8,0n C r = 1,2m