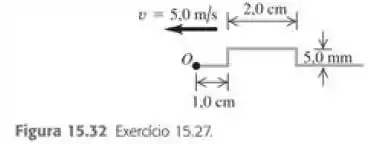
Um pulso ondulatório deslocando-se sobre uma corda para possui as dimensões indicadas na Figura 15.32. A velocidade da onda é igual a 5 m/s. a) Se o ponto O for uma extremidade fixa, desenhe a onda total sobre a corda para ,, 4,0, e e . b) Repita o item (a) quando o ponto for uma extremidade livre.
Passo 1
A distância que a forma da onda viaja no tempo é . O pulso da onda reflete no final da corda, em ponto . Logo vamos calcular o deslocamento da onda para cada tempo e descobrir onde ela está:
- No primeiro intervalo de tempo, quando , a distância percorrida será:
- No intervalo de tempo , a distância percorrida será:
- No intervalo de tempo , a distância percorrida será:
- No intervalo de tempo , a distância percorrida será:
- No intervalo de tempo , a distância percorrida será:
- No intervalo de tempo , a distância percorrida será:
- No intervalo de tempo , a distância percorrida será:
- No primeiro intervalo de tempo, quando , a distância percorrida será:
- No primeiro intervalo de tempo, quando , a distância percorrida será:
- No intervalo de tempo , a distância percorrida será:
- No intervalo de tempo , a distância percorrida será:
- No intervalo de tempo , a distância percorrida será:
- No intervalo de tempo , a distância percorrida será:
- No intervalo de tempo , a distância percorrida será:
Substituindo o tempo e a velocidade que conhecemos :
Então nossa onda andou 0,5 cm, isso encurtou a distância entre ela e o ponto O em:
Logo nosso desenho será:
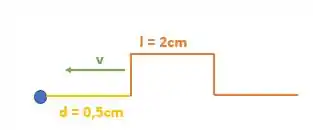
Perceba que a nossa onda continua com o mesmo tamanho e a velocidade também continua igual.
Substituindo o tempo e a velocidade que conhecemos :
Então nossa onda andou 1 cm, isso encurtou a distância entre ela e o ponto O em:
Logo nosso desenho será:
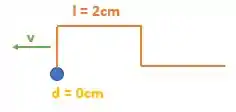
Ou seja, a onda já chegou no ponto O, quando ela chega nesse ponto fixo, ele não se moverá, mas absorverá a energia.
Substituindo o tempo e a velocidade que conhecemos :
Então nossa onda andou 1,5 cm, isso que dizer que não existe mais distância entre o ponto O e a onda. Agora a energia da onda está sendo absorvida e logo isso irá gerar uma reação.
Por outro lado, se a onda se deslocou esse 1,5 cm e o ponto O estava a 1cm de distância. O que acontece com esse deslocamento extra de 0,5cm? Bom ele será encurtado da onda:
Então nosso desenho ficará da seguinte forma:
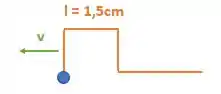
Substituindo o tempo e a velocidade que conhecemos :
Se a onda se deslocou esse 2,0 cm e o ponto O estava a 1cm de distância. O que acontece com esse deslocamento extra de 1,0cm? Bom ele será encurtado da onda:
Então nosso desenho ficará da seguinte forma:
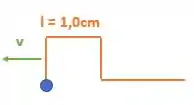
Substituindo o tempo e a velocidade que conhecemos :
Se a onda se deslocou esse 2,5 cm e o ponto O estava a 1cm de distância. O que acontece com esse deslocamento extra de 1,5cm? Bom ele será encurtado da onda:
Então nosso desenho ficará da seguinte forma:
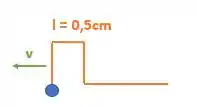
Substituindo o tempo e a velocidade que conhecemos :
Se a onda se deslocou esse 3,0 cm e o ponto O estava a 1cm de distância. O que acontece com esse deslocamento extra de 2cm? Bom ele será encurtado da onda:
Então nosso desenho ficará da seguinte forma:

Ou seja, toda a energia da onda foi absorvida nesse ponto, essa força que a onda produz no ponto que não se movimenta, gera uma força contrária. Essa força contrária que é responsável por gerar um pulso refletido invertido que veremos no próximo instante de tempo.
Substituindo o tempo e a velocidade que conhecemos :
Se a onda se deslocou esse 3,5 cm e o ponto O estava a 1cm de distância. O que acontece com esse deslocamento extra de 2,5cm? Bom ele será refletido:
Então nosso desenho ficará da seguinte forma:
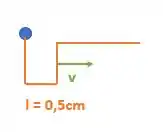
O pulso de onda foi refletido invertido e viaja a mesma velocidade no sentido contrário com a mesma amplitude. Se continuássemos os próximos instantes de tempo, veríamos a mesma forma de onda refletida e invertida andando pela corda.
Passo 2
A diferença entre a extremidade ser fixa ou ser livre é que o pulso refletido é invertido quando é uma extremidade fixa e não é invertido quando é uma extremidade livre. Vamos fazer o passo a passo que fizemos no item anterior que eu vou mostrar melhor isso.
Substituindo o tempo e a velocidade que conhecemos :
Então nossa onda andou 0,5 cm, isso encurtou a distância entre ela e o ponto O em:
Logo nosso desenho será igual no primeiro caso:
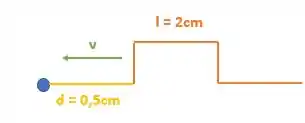
Substituindo o tempo e a velocidade que conhecemos :
Então nossa onda andou 1 cm, isso encurtou a distância entre ela e o ponto O em:
O que varia nesse caso, é que o ponto O irá se mover para o topo da onda:
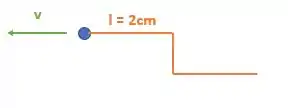
Substituindo o tempo e a velocidade que conhecemos :
Então nossa onda andou 1,5 cm, isso que dizer que não existe mais distância entre o ponto O e a onda. Agora a energia da onda está sendo absorvida e logo isso irá gerar uma reação.
Por outro lado, se a onda se deslocou esse 1,5 cm e o ponto O estava a 1cm de distância. O que acontece com esse deslocamento extra de 0,5cm? Bom ele será encurtado da onda:
O ponto O continua no topo da onda. Então nosso desenho ficará da seguinte forma:
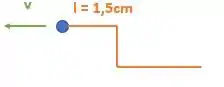
Vamos continuar fazendo isso para os próximos casos.
Substituindo o tempo e a velocidade que conhecemos :
Se a onda se deslocou esse 2,0 cm e o ponto O estava a 1cm de distância. O que acontece com esse deslocamento extra de 1,0cm? Bom ele será encurtado da onda:
Então nosso desenho ficará da seguinte forma:
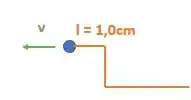
Substituindo o tempo e a velocidade que conhecemos :
Se a onda se deslocou esse 2,5 cm e o ponto O estava a 1cm de distância. O que acontece com esse deslocamento extra de 1,5cm? Bom ele será encurtado da onda:
Então nosso desenho ficará da seguinte forma:
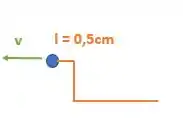
Substituindo o tempo e a velocidade que conhecemos :
Se a onda se deslocou esse 3,0 cm e o ponto O estava a 1cm de distância. O que acontece com esse deslocamento extra de 2cm? Bom ele será encurtado da onda:
Então nosso desenho ficará da seguinte forma:
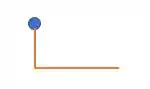
Ou seja, toda a energia da onda foi absorvida nesse ponto, essa força que a onda produz no ponto O fez com que esse ponto se movimentasse, gera uma força contrária. Essa força contrária que é responsável por gerar um pulso refletido que veremos no próximo instante de tempo.
Substituindo o tempo e a velocidade que conhecemos :
Se a onda se deslocou esse 3,5 cm e o ponto O estava a 1cm de distância. O que acontece com esse deslocamento extra de 2,5cm? Bom ele será refletido:
Então nosso desenho ficará da seguinte forma:
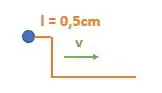
Veja que o pulso foi refletido, mas dessa vez como temos uma extremidade livre, o pulso não é invertido.
Pronto, acabamos com essa questão!
Resposta
