Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 15.Problemas - Ex. 56
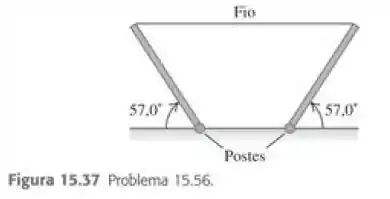
Um fio de 5,0 m e 0,732 kg é usado para sustentar dois postes uniformes de 235 N de igual comprimento (Figura 15.37). Suponha que o fio esteja na horizontal e que a velocidade do som seja 344 m/s. Um vento forte está soprando, fazendo com que o fio vibre em seu sétimo sobretom. Quais são a frequência e o comprimento de onda do som que esse fio produz?
Passo 1
E aí galera?!
Vamos aplicar para um poste e calcule a tensão no fio.
por ondas no fio. .
A onda estacionária no fio e o som que produz têm a mesma frequência. Para ondas estacionárias no fio
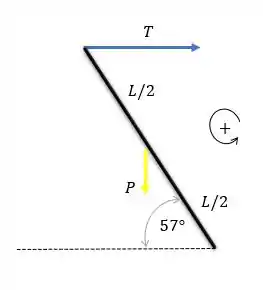
Para o sétimo harmônico, . O fio possui . O diagrama de corpo livro de um dos posts é apresentado abaixo. As forças no pivô não são mostradas. Tomamos o eixo de rotação para estar no pivô, então as forças no pivô não produzem torque.
Passo 2
Nos diz que:
Para ondas no fio,
Passo 3
Para a sétima onda estacionária de harmônicos no fio,
As ondas sonoras têm frequência 18,3 Hz e comprimento de onda
A frequência da onda sonora está no limite inferior das frequências audíveis. O comprimento de onda da onda estacionária no fio é muito menor que o comprimento de onda das ondas sonoras, porque a velocidade das ondas no fio é muito menor que a velocidade do som no ar.