Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 45
Um radar estacionário indica que um navio está 10 km ao sul dele. Uma hora depois, o mesmo navio está 20 km a sudeste. Se o navio se deslocou com rapidez constante e sempre no mesmo sentido, qual era sua velocidade nesse tempo?
Passo 1
Oi pessoal, tudo bem?
Vamos desenhar o que o enunciado falou, colocando o radar na origem do eixo de um sistema de coordenadas e desenhando os dois pontos onde o navio é detectado:
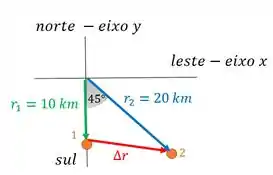
Percebe que a gente colocou também os vetores posições e que indicam as posições 1 e 2 do navio. E que quando ele fala sudeste, quer dizer uma orientação a de leste indo para sul.
A partir dessa situação, ele pede a velocidade do barco no tempo entre esses dois instantes. Como a rapidez do barco foi constante (o módulo da velocidade foi constante), a gente pode dizer que a velocidade foi igual a velocidade média. Ela tem essa expressão vetorial:
Sendo que é o tempo decorrido. O enunciado diz que o deslocamento aconteceu em 1 hora. Então
E é o vetor deslocamento do barco, que é dado pela diferença entre o vetor posição da segunda posição menos o vetor do posição da primeira posição:
Substituindo esses dois na nossa velocidade:
A ideia é a gente usar essa expressão para achar a velocidade do nosso barquinho. Vamos lá!
Passo 2
Vamos aplicar ao nosso problema:
Precisamos dos vetores e . Achamos esses carinhas pela nossa figura. Para a posição 1:
Já que a primeira posição está abaixo da origem. E para a posição 2 vamos achar as componentes de por trigonometria:
Usamos seno para o eixo pois o ângulo de está colado nesse eixo. E a componente é negativa pois estamos na parte negativa de .
Fazendo a continha:
Passo 3
Agora é calcular:
Então, temos que a velocidade do barco é