Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 35.4 - Ex. 50
Reflexão em filmes finos. Na Fig. 35-41, a luz incide perpendicularmente em um filme fino de um material 2 que está entre as placas (espessas) dos materiais 1 e 3. (Os raios foram desenhados com uma pequena inclinação apenas para tornar a figura mais clara.) As ondas representadas pelos raios e interferem de tal forma que a intensidade da onda resultante pode ser máxima (máx) ou mínima (mín).
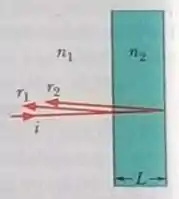
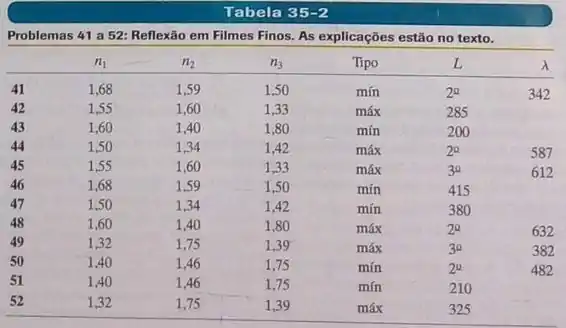
Para esta situação, os dados da Tabela 35-2 se referem aos índices de refração , e , ao tipo de interferência, à espessura do filme fino em nanômetros e ao comprimento de onda em nanômetros da luz incidente, medido no ar. Nos problemas em que não é dado o comprimento de onda , pede-se o valor de que está na faixa da luz visível; nos problemas em não é dada a espessura , pede-se a segunda menor espessura ou a terceira menor espessura, de acordo com a indicação da tabela.
Passo 1
A questão trata sobre interferência em filmes finos. Nesse problema, temos que e . Assim, nas duas reflexões ocorrem inversão de fase, de modo que podemos desconsiderá-las completamente:
Como , temos que
Passo 2
O exercício pede um mínimo de interferência, de modo que
Logo,
Sabemos que
Assim,
Como queremos a segunda menor espessura, tomamos :
*A menor espessura ocorre para .