Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 34.Problemas - Ex. 92
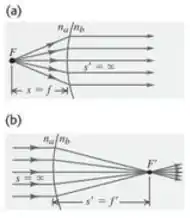
Para a refração em uma interface esférica, a primeira distância focal é definida como o valor de correspondnente a , como na figura (a). A segunda distância focal é defnida como o valor de correspondente a , como indicado na figura (b). (a) Prove que a relação geral entre a distância do objeto e a distância da imagem é dada por
Passo 1
A fórmula para a refração no caso da interface esférica é a seguinte:
No primeiro caso, as variáveis vão ter esses valores aqui:
Então:
E no segundo caso os valores são:
Ou seja:
Beleza, isso dá um sistema de duas equações que a gente pode resolver pra achar aquelas identidades:
Os termos que tem “infinito” no denominador vão sumir:
Passo 2
(a) Nosso primeiro objetivo é provar que:
Essa é fácil, só temos que dividir uma equação pela outra no nosso sistema:
Beleza, demonstrado.
Passo 3
(b) E a última tarefa é provar essa relação aqui:
E o truque pra fazer isso é o seguinte: primeiro a gente volta lá na equação original:
E aí a gente substitui usando a fórmula que a foi provada ali em cima (poderia substituir também):
Então:
Já dá pra cortar dos dois lados:
Agora vamos multiplicar os dois lados por :
Passo 4
Pra sair dessa situação, vamos voltar lá no nosso sistema:
Reorganizando ele um pouco:
Fazendo a segunda equação menos a primeira:
Ótimo, agora é só substituir isso na equação lá de cima:
Pronto! Demonstramos o que o enunciado pediu.
Resposta
(a) Demonstração.
(b) Demonstração.