Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 34.Problemas - Ex. 94
Na figura abaixo, a vela está no centro de curvatura do espelho côncavo cuja distância focal é . A lente convergente possui distância focal igual a e está a uma distância de à direita da vela. A vela é vista através da lente por um observador situado à direita da lente. A lente forma duas magens da vela. A primeira é formada pela luz que passa diretamente através da lente. A segunda é formada pela luz que passa pela lente atinge o espelho, é refletida e a seguir passa novamente pela lente. (a) Faça um diagrama dos raios principais mostrando a localização de cada uma dessas imagens. (b) Para cada uma das imagens, responda: i) onde está a imgem? ii) a imagem é real ou virtual? iii) a imagem final é dirita ou invertida em relação ao objeto original?
Passo 1
(a) Vamos começar desenhando o diagrama dos raios principais para o caso da luz que passa pela lente:
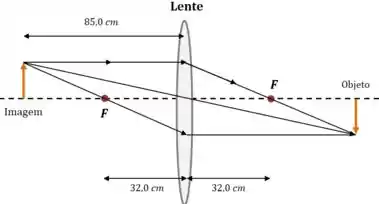
Nesse desenho só o que a gente fez foi desenhar três raios notáveis:
O primeiro passa pelo foco do lado esquerdo e segue paralelo ao eixo da lente.
O segundo segue paralelo ao eixo da lente e então passa pelo foco do lado direito.
O terceiro passa pelo centro da lente e simplesmente segue reto.
O ponto onde esses três raios se encontram já nos diz como a imagem se forma.
Passo 2
(b) Agora vamos fazer a mesma coisa para o espelho côncavo:
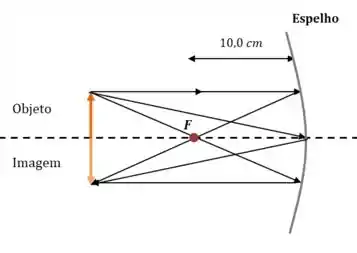
Mais uma vez, só o que a gente fez foi desenhar três raios principais:
O primeiro passa pelo foco e volta paralelo ao eixo do espelho.
O segundo segue paralelo ao eixo do espelho e então volta passando pelo foco.
O terceiro atinge o centro de curvatura e é refletido com o mesmo ângulo.
Passo 3
(b) Agora vamos começar com as contas. Primeiro para a imagem formada pela lente.
(i) Pra descobrir a posição da imagem é só usar essa fórmula aqui:
(ii) Já que , a imagem é real.
(iii) Pra descobrir se a imagem é direita ou invertida, temos que calcular a ampliação :
Como a ampliação é negativa, a imagem é invertida.
Passo 4
Agora vamos pensar na imagem que é refletida pelo espelho e só depois passa pela lente.
Uma grande vantagem aqui é que o nosso desenho já mostrou que o espelho côncavo simplesmente inverte a imagem.
Obs.: isso acontece sempre que o objeto está em cima do centro de curvatura do espelho côncavo, como nesse caso.
(i) Então beleza, depois de ser refletida pelo espelho, a imagem é simplesmente invertida, e então, quando passar pela lente, a imagem gerada vai estar na mesma posição de antes:
(ii) Mais uma vez, ficamos com , então a imagem é real.
(iii) E a ampliação também continua igual:
Como esse sinal é negativo, isso quer dizer que a lente inverte a imagem mais uma vez. Já que o espelho também tinha invertido, essa imagem acaba sendo direita em relação ao objeto original.
Resposta
(a) Desenho.
(b) No primeiro caso: (i) , (ii) A imagem é real e (iii) imagem invertida. No segundo caso: (i) , (ii) A imagem é real e (iii) imagem direita.