Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 106
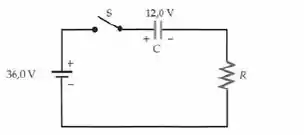
Repita o problema 105 para o caso da polaridade inicial do capacitor ser oposta a mostrada na figura abaixo.
Passo 1
Essa questão já diz tudo né? Hoje é dia de flashback rs
Usaremos o mesmo raciocínio da questão anterior, a única coisa que mudará será o sinal da tensão do capacitor quando aplicarmos a segunda lei de kirchoff’s, pois a polaridade dele está invertida. Observe:
Passo 2
Aplicando a Segunda Lei de Kirchhoff’s imediatamente após a chave do circuito for fechada:
Igual a alternativa (a) da questão 105, a única coisa que mudou foi o sinal do , esse fator ocasionou uma corrente diferente, logo, o resultado da alternativa (b) também será diferente daquele obtido na questão passada, confere só.
Passo 3
Para a resolução da (b) aplicaremos a Segunda Lei de Kirchhoff’s quando a tensão no capacitor for igual a e resolveremos para (tensão no resistor):
Agora expressando a correndo em função de e :
Sabendo que , podemos substituir isso na equação:
Viu como mudou? enfim, por hoje é só, até a próxima!
Resposta
a)
b)