Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Problemas - Ex. 101b
Repita o problema considerando que a placa é positiva.
Passo 1
Cada placa gera um campo elétrico em volta delas que depende do sinal da carga ou, no caso, da densidade superficial de carga . Lembrando que o campo é dado por:
Supondo que as placas são anelares e infinitas, o campo é dado como:
Onde . Também podemos perceber que o campo elétrico agora não depende mais da distância entre elas e do ponto de teste.
Assim, pelo princípio da superposição dos campos elétricos, o campo resultante entre as placas será o resultado da interação entre ambos.
Passo 2
Com isso, temos que para a placa :
E para a placa :
Importante lembrar que o sinal representa o sentido do campo elétrico.
Passo 3
Fazendo o esboço da situação:
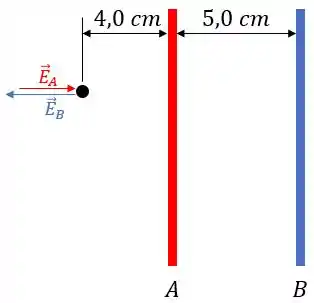
Os campos irão se subtrair por estarem sentidos contrários. Então, como o campo de tem uma maior intensidade:
para a esquerda.
Resposta
para a esquerda