Uma lente convergente tem distância focal de . (a) Usando uma planilha eletrônica ou calculadora gráfica, faça um gráfico da distância imagem como função da distância objeto para distâncias objeto variando de até , onde é a distância focal. (b) No mesmo gráfico usado na Parte (a), mas usando um eixo diferente, faça um gráfico da ampliação da lente como função da distância objeto. (c) Que tipo de imagem é produzido para este intervalo de distância objeto – real ou virtual, direita ou invertida? (d) Discuta o significado de quaisquer limites assintóticos que seus gráficos apresentarem.

Para a parte (a); Primeiramente utilizaremos a equação das lentes delgadas para obter a expressão que usaremos para calcular , observe:

A ampliação será determinada pela equação:

Logo abaixo mostraremos um programa que irá calcular como uma função de . As formulas utilizadas para calcular as quantidades nas colunas são as demonstradas na imagem abaixo (Você pode testar isso no Exceel, se quiser):

Será calculada uma quantidade de 111 dados:

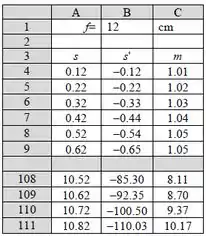
Com esses dados, estabelecemos um gráfico, e como funções:

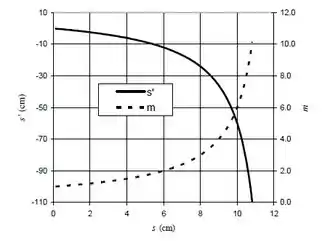
FEITA A PARTE (A) e (B), vamos continuar...

Bem amigo, a parte(c) é o seguinte, as imagens são reais e direitas para essa gama de distâncias objetos; Para a parte (d) diremos que, as equações para os assintóticos do gráfico de versus , é . Ela indica que se um objeto avança para o segundo ponto focal, a ampliação da distância imagem se torna grande sem limites; As equações para os assintóticos horizontais e verticais do gráfico de versus , é . Essa indica que se um objeto avança para o segundo ponto focal a imagem se torna grande sem limites. Em soma, quando se aproxima de zero, se aproxima de infinito negativo e se aproxima de , então quando um objeto avança em direção as lentes, a imagem se torna do mesmo tamanho que o objeto e a distância imagem cresce sem limites.

PROBLEMA RESOLVIDO! Foi mais tranquilo do que esperava né? Hehe isso aí, bons estudos! até a próxima.