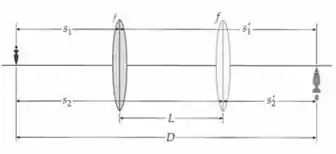
Você está trabalhando para um especialista em óptica durante o verão. Ele precisa medir uma distância focal desconhecida e você sugere usar o método de Bessel (veja o Problema 57), que você utilizou durante um laboratório de física. Você define a distância objeto-imagem como 1.70 m. A posição da lente é ajustada para obter uma imagem definida no anteparo. Uma segunda imagem definida é encontrada quando a lente é movida por 72 cm a partir da primeira posição. (a) Esboce o diagrama de raios para as duas posições. (b) Determine a distância focal da lente usando o método de Bessel. (c) Quais são as duas posições da lente com relação ao objeto? (d) Quais são as ampliações das imagens quando a lente está nas duas posições?  

 

Para a parte (a), usaremos as distâncias utilizadas no Problema 57 para desenhar o seguinte diagrama: 

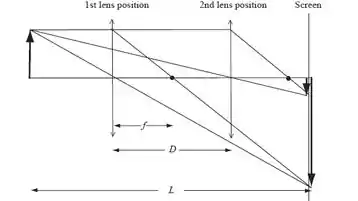
Agora vamos para a parte (b) 

Na parte (b) aplicaremos os valores dados no problema na equação (1), dessa forma: 

Agora, parte (c)! 

Na parte (c), para determinarmos as duas posições da lente utilizaremos a equação (2) e (3), de tal forma que: 

Substituindo as variáveis pelos valores numéricos fornecidos pela questão, temos: 

Feito isto, agora vamos para a última (mas não menos importante) parte! 

Utilizaremos a equação (4) e as expressões e (obtidas no problema 57), para obtermos as ampliações tanto da primeira quando da segunda lente: 

PRONTINHO, fizemos todas! Obrigado, até a próxima, fica bem!