Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 32.1 - Ex. 59
Um objeto está a à esquerda de uma lente que tem distância focal de . Uma segunda lente, que tem distância focal de , está a à direita da primeira lente. (a) Determine a distância entre o objeto e a imagem final formada pela segunda lente. (b) Qual é a ampliação total? (c) A imagem final é real ou virtual? Ela é direita ou invertida?
Passo 1
HELLO GALERA, vamos resolver mais um problema, primeiro, analise o diagrama de raios abaixo:
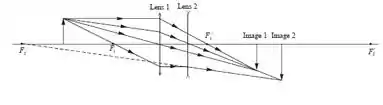
O diagrama nos mostra quatro raios da cabeça do objeto que encontra as imagens e . Podemos usar a equação das lentes delgadas para encontrar a posição da imagem formada nas lentes positivas e então, sabendo o valor da distância que separa as duas lentes, determinaremos a distância do objeto em relação à segunda lente e aplicar a equação das lentes delgadas uma segunda vez para encontrar a posição da imagem final.
Passo 2
Primeiro, começaremos expressando a distância do objeto para imagem:
(1)
Começaremos aplicando a equação das lentes delgadas na lente positiva:
Substituindo as variáveis por valores numéricos, temos:
Encontrando a distância objeto para lentes negativas:
A distância imagem é dada por:
Substituindo as variáveis por valores numéricos, temos:
Substituindo os termos na equação (1) e calculando d:
Dessa forma, descobrimos que a imagem final está à direita da segunda lente. Agora, vamos para a parte (b)!
Passo 3
Para a parte (b), sabemos que a ampliação lateral total é dada por:
Expressaremos e , logo:
Substituindo as variáveis pelos valores numéricos, temos:
Agora, iremos para a letra (c) e assim finalizaremos a questão!
Passo 4
Para a letra (c), por conta de , a imagem é invertida, e por conta de , a imagem é real.
PROBLEMA FINALIZADO, fiquem bem, bons estudos e até a próxima
Resposta
a)
b)
c) Invertida e real