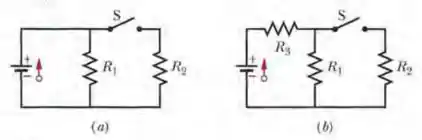
As resistências das Figs. 27-45a e 27-45b são todas de e as fontes ideais são baterias de . (a) Quando a chave da Fig. 27-45a é fechada, qual é a variação da diferença de potencial entre os terminais do resistor ? (b) Quando a chave da Fig. 27-4Sb é fechada, qual é a variação da diferença de potencial entre os terminais do resistor ?

(a) De acordo com a regra das malhas, a diferença de potencial não varia quando a chave é fechada.

O objetivo deste item é verificar se o aluno apreendeu corretamente o conceito de tensão. Alguns estudantes confundem os conceitos de tensão e corrente e pensam que a tensão é dividida entre dois resistores em paralelo, o que seria difícil de conciliar com a resposta correta.

Tranquilo até aqui? 😊

A regra das malhas continua válida, é claro, mas, neste caso, de acordo com a regra dos nós e a lei de Ohm, as quedas de tensão em e , que eram iguais antes do fechamento da chave, passam a ser diferentes.

Como uma corrente maior atravessa a bateria, a queda de tensão em aumenta. Como, de acordo com a regra das malhas, a soma das quedas de tensão em e em é igual à tensão da bateria, isso significa que a queda de tensão em diminui.

Como e têm o mesmo valor, quando a chave estava aberta, a queda de tensão em era

De acordo com a Eq. 27-24, com a chave fechada, a resistência equivalente de e é , o que significa que a resistência total entre os terminais da bateria é

A corrente é, portanto

O que significa que a queda de tensão em é

Nesse caso, de acordo com a regra das malhas, a queda de tensão em é

Assim, a variação da diferença de potencial quando a chave é fechada é

Sacou tudo? Responde Aí! 😊