Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 25.Problemas Desafiadores - Ex. 85

A resistividade de um semicondutor pode ser alterada adicionando-se diferentes quantidade de impurezas. Uma barra de um semicondutor de comprimento L e seção reta com área A está ao longo do eixo Ox, entre x=0 e x=L. O material obedece à lei de Ohm e sua resistividade varia ao longo da barra, de acordo com a relação ρ x = ρ 0 exp ⁡ - x L . A extremidade da barra para x=0 está a um potencial V 0 mais elevado do que o potencial da extremidade x=L. (a) Calcule a resistência total da barra e a corrente que flui através dela. (b) Determine o modulo do campo elétrico E(x) na barra em função de x. (x) Faça um gráfico das funções ρ x , E(x) e V(x) para valores de x de compreendidos entre x=0 e x=L.

Passo 1

E aí galera, aqui aplicaremos

R = ρ L A

para encontrar a resistência de uma fatia fina da haste e integrar para encontrar o R total.

Lembremos que V = I R .

Encontraremos também R ( x ) , a resistência de um comprimento   x da haste.

E x = ρ x J

Passo 2

  1. Assim, a resistência total da barra e a corrente que flui através dela é dada por:

    2. d R = ρ d x A = ρ 0 exp ⁡ - x / L d x A

    Então,

    R = ρ 0 A   ∫ 0 L exp ⁡ - x L   d x = ρ 0 A   - L exp ⁡ [ - x L ]   0 L = ρ L A 1 - e - 1

    E

    I = V 0 R = V 0 A ρ 0 L ( 1 - e - 1 )

    Com um limite superior de x   em vez de   L na integração,

    R x = ρ 0 L A ( 1 - e - x / L )

    Passo 3

  2. E E x é dado por:

    3. E x = ρ x J = I ρ 0 e - x / L A = V 0 e - x / L L ( 1 - e - 1 )

    Passo 4

  3. E V :

    4. V = V 0 - I R x

    V = V 0 - V 0 A ρ 0 L 1 - e - 1 ρ 0 L A ( 1 - e - x / L ) = V 0 ( e - x / L - e - 1 ) ( 1 - e - 1 )

    Passo 5

  4. Gráficos de resistência, campo elétrico e potencial de x   =   0   a   L são dados na Figura abaixo. Cada quantidade é dados em termos da unidade indicada.

Resistividade ( ρ 0 )

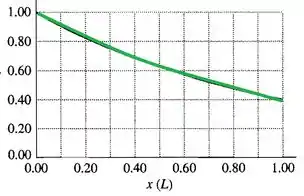
Campo elétrico V 0 L

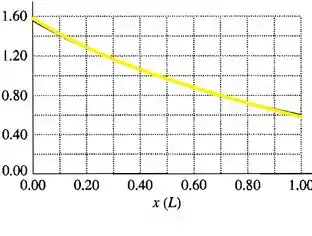
Potencial ( V 0 )

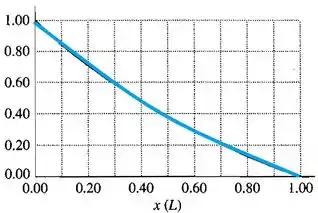
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

53- No circuito indicado na Figura 25.39 , calcule ( a ) a taxa de conversão de energia interna (química) em energia elétrica no interior da bateria ( b ) a taxa de dissipação da energia elétrica na b
49- A capacidade de uma bateria com acumuladores, tal como a usada no sistema elétrico do automóvel, é especificada em ampéres-horas (A.h). Uma bateria de 50A pode forncecer uma corrente de 50A durant
48- Considere o circuito da Figura 25.37 . ( a ) Qual é a taxa total da dissipação da energia elétrica nos resistores de 5.0Ω e de 9.0Ω ? ( b ) Qual é a potência fornecida pela bateria de 16.0V ? ( c
69- A diferença de potencial nos terminais de uma bateria é igual a 8.4V quando uma corrente igual a 1.50A flui do terminal negativo para o terminal positivo da bateria. Quando a corrente é igual a 3.
71- A resistividade volumétrica média do corpo humano (sem considerar a resistência da pele) é aproximadamente igual a 5.0Ω . O caminho para a condução entre as mãos pode ser visto como um cilindro co