Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 38

Um rifle com cano de 60   c m de comprimento dispara uma bala de 10   g com velocidade horizontal de 400   m / s . A bala atinge um bloco de madeira e penetra 12   c m no material.

  1. Que valor de força resistiva (considerada constante) a madeira exerce sobre a bala?
  2. Quanto tempo leva para a bala atingir o repouso?
  3. Trace um gráfico velocidade versus tempo para a bala dentro da madeira.

Passo 1

Vamos representar o que está acontecendo dentro da madeira:

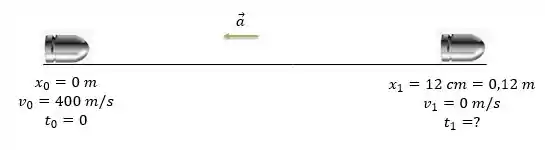
Quando a bala atinge a madeira, ela passa a sofrer uma aceleração no sentido oposto ao movimento até que ela pare após penetrar 12   c m da madeira.

Passo 2

  1. Que valor de força resistiva (considerada constante) a madeira exerce sobre a bala?

    2. Para encontrar a força resistiva que a madeira exerce sobre a bala podemos utilizar a 2 ° lei de Newton:

    F r e s i s t = m a

    Mas para isso precisamos achar qual é o valor da aceleração da bala quando está penetrando a madeira.

    Para achar a aceleração vamos utilizar a equação de Torricelli:

    v 1 2 = v 0 2 + 2 a ( ∆ x )

    v 1 2 = v 0 2 + 2 a ( x 1 - x 0 )

    a = v f 2 - v i 2 2 ( x 1 - x 0 )

    a = 0 2 - 400 2 2   x   ( 0,12 - 0 ) = - 6,67 × 10 5   m / s 2

    Passo 3

    Conhecida a aceleração podemos retornar à 2 ° lei de Newton e encontrar a força resistiva:

    F r e s i s t = m a

    A massa foi fornecida:

    m = 10   g = 0,01   K g

    Obs.: A massa precisa estar em K g para a força ser expressa em Newton.

    Logo,

    F r e s i s t = 0,01   x   - 6,67 × 10 5

    F r e s i s t = - 6   670   N

    Passo 4

  2. Quanto tempo leva para a bala atingir o repouso?

    3. Vamos achar o tempo vamos utilizar a fórmula:

    v 1 = v 0 + a ∆ t

    ∆ t = v 1 - v 0 a

    Substituindo os valores:

    ∆ t = 0 - 400 - 6,67 × 10 5 = 6 × 10 - 4   s = 600   × 10 - 6   s = 600   μ s

    Passo 5

  3. Trace um gráfico velocidade versus tempo para a bala dentro da madeira.

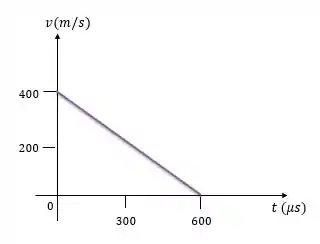
Como a aceleração da bala penetrando a madeira é constante, o gráfico de velocidade versus tempos será uma reta.

No tempo zero a velocidade é de 400   m / s e no tempo final, t = 600   μ s , a velocidade é zero.

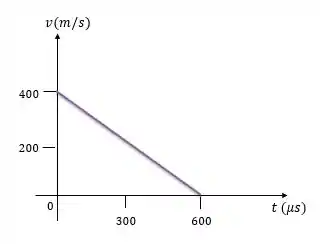
Resposta

  1. F r e s i s t = - 6   670   N
  2. ∆ t = 600   μ s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um homem de 80 kg puxa seu filho de 40 kg com uma força de 100 N, os dois de patins sobre o gelo. Juntos , eles deslizam sobre o gelo ganhando rapidez a uma taxa constante. (a) A força exercida pelo m
Explique por que, das interações fundamentais, é a interação gravitacional a que mais nos afeta no dia-a-dia. Da lista, há uma outra que representa um papel cada vez maior tendo em vista a nossa tecno
Um carro de competição descontrolado freia até 90 km/h antes de bater de frente contra uma parede de tijolos. Por sorte, o piloto está usando o cinto de segurança. Usando valores razoáveis para a mass
Um rebocador puxa um navio com uma força constante de magnitude F 1 . O aumento da rapidez do navio durante um intervalo de 10 s é de 4,0 km/h. Quando um segundo rebocador aplica uma força constante a
Uma partícula viaja em linha reta com a rapidez constante de 25,0 m/s. Repentinamente, uma força de 15,0 N age sobre ela, levando-a ao repouso em uma distância de 62,5 m. (a) Qual é a orientação da fo