Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.10 - Ex. 64
Em , uma roda tem uma velocidade angular de , uma aceleração angular constante de e uma reta de referência em . (a) Qual é o maior ângulo descrito pela reta de referência no sentido positivo? Qual é (b) o primeiro e (c) o segundo instante no qual a reta de referência passa pelo ângulo ? Em que (d) instante negativo e (e) instante positivo a reta de referência passa pelo ângulo ? (f) Faça um gráfico de em função de e indique as respostas dos itens (a) a (e) no gráfico.
Passo 1
No instante em que a roda para momentaneamente de girar no sentido positivo antes de começar a girar no sentido negativo é onde o ângulo com . Podemos usar a equação Eq. 10-14:
isolando e substituindo temos:
Passo 2
Bom pessoal , de acordo com a Eq. 10-13, temos:
Podemos usar essa equação para conseguir descobrir o valor do instante no qual a reta de referência passa pelo ângulo .
Fazendo , e substituindo na equação temos:
ou
Assim, o primeiro instante em que a reta de referência passa pelo ângulo é e o segundo instante é .
Passo 3
Bom galera , vamos usar a mesma equação Eq. 10-13 do passo 2:
Fazendo , e substituindo na equação temos:
ou
Assim, o instante negativo em que a reta de referência passa pelo ângulo é e o instante positivo é .
Passo 4
De acordo com o resultado do item (d)
O gráfico pedido é mostrado na figura a seguir, com os resultados dos itens anteriores assinalados por pontos.
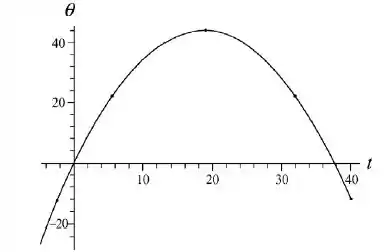
Resposta
(a)
(b)
(c)
(d)
(e)
(f)
Tranquilo galera? Bora resolver mais questões então ☺