Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 9.Problemas - Ex. 12a
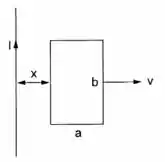
Uma espira retangular de lados e b afasta-se com velocidade de um fio retilíneo muito longo, que transporta corrente contínua de intensidade . A espira tem resistência e autoindutância desprezível. No instante considerado, sua distância ao outro fio é (fig.).
- Calcule o fluxo de através da espira nesse instante.
Passo 1
Vamos começar lembrando que o fluxo é dado por
onde o campo do fio é
Observe o desenho para entender os próximos passos.
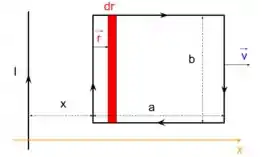
Pela figura podemos ver que
e
Passo 2
Agora precisamos montar nossa integral
Resposta
Exercícios de Livros Relacionados
Uma bobina circular tem 25 voltas e raio de 5,0 c m . Ela está no equador, onde o campo magnético da Terra é 0,70 G , apontando para o norte. O eixo da bobina é a linha que passa pelo seu centro e é p
Determine o fluxo magnético através de um solenoide de 800 voltas que tem comprimento igual a 30,0c m , raio igual a 1,00c m e conduz uma corrente de 2,00 A .
Um condutor cilíndrico longo com raio R e comprimento L conduz uma corrente I . Determine o fluxo magnético por unidade de comprimento através da área indicada na Figura 28-44.
Um longo solenoide tem n voltas por unidade de comprimento, raio R 1 e conduz uma corrente I . Uma bobina circular de raio R 2 e com N voltas é coaxial ao solenoide e está equidistante de suas extremi
Uma bobina circular tem 15,0 voltas, raio de 4,0c m e está em um campo magnético uniforme de 4,0k G na direção + x . Determine o fluxo através da bobina quando a normal unitária do plano da bobina é a