Seja . Determine os componentes e de em cada um dos sistemas de coordenadas mostrados na FIGURA EX3.18.
Passo 1
Vamos começar com o sistema de coordenadas (a) porque é aquele convencional, que já estamos acostumados, beleza?
Vamos desenhar o vetor no sistema de coordenadas (a):
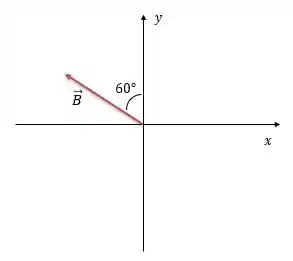
Pronto, temos o vetor , fazendo um ângulo de com a vertical, e está no segundo quadrante porque a questão nos disse que esse ângulo era partindo na vertical e caminhando no sentido anti-horário, beleza?
Passo 2
Para calcular as componentes vamos usar aquele macetinho esperto:
A componente que está COlada com o ângulo é igual ao módulo do vetor vezes o COsseno do ângulo. Já a componente que está SEparada do ângulo é igual ao módulo do vetor vezes o SEno do ângulo.
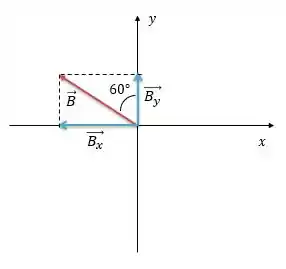
Nota que para a componente tem um sinal de negativo acompanhando. Esse sinal é pra indicar que essa componente está apontando no sentido contrário ao sentido do eixo . Beleza?
A questão nos deu o módulo do vetor:
E sabemos que:
Então, as componentes serão:
Lembrando que temos os vetores unitários e para representar as direções dos eixos e , respectivamente, podemos escrever o vetor assim:
Passo 3
Agora, vamos para o sistema de coordenadas (b), aquele que não estamos acostumados.
Vamos desenhar o vetor nesse sistema:
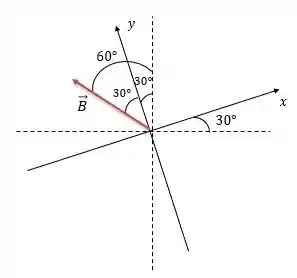
Vamos lá, o vetor faz um ângulo de com a vertical no sentido anti-horário, mas agora o sistema de coordenadas foi rotacionado em no sentido anti-horário, isso quer dizer que ele faz um ângulo de com a horizontal e com a vertical no sentido anti-horário. E é isso que está mostrando a figura acima, beleza?
O ângulo que o vetor faz com o eixo do sistema de coordenadas é de porque fazemos , como a figura também mostra.
Agora que sabemos o ângulo que o vetor faz com o eixo podemos achar as componentes.
Passo 4
Aquele mesmo macete para calcular as componentes:
COlado – COsseno, SEparado – SEno
Já sabemos o módulo:
E sabemos que:
Então:
Escrevendo em termos de e :
Resposta
Sistema de coordenadas (a):
Sistema de coordenadas (b):