Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 19
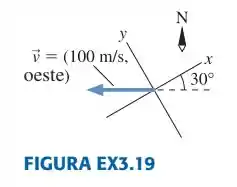
Quais são os componentes e do vetor velocidade mostrado na FIGURA EX3.19?
Passo 1
Para acharmos as componentes de um vetor precisamos saber o ângulo que o vetor faz com pelo menos um dos eixos do sistema de coordenadas, então o que precisamos achar primeiro é exatamente esse ângulo.
Olha aqui a imagem:
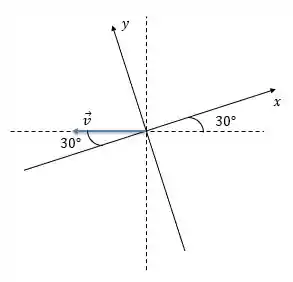
O semi-eixo positivo do sistema de coordenadas faz um ângulo de com a horizontal e consequentemente, o semi-eixo negativo também faz. Como o vetor está na horizontal, ele também faz um ângulo de com o semi-eixo negativo, belezinha?
Agora que sabemos o ângulo que o vetor faz com o eixo podemos achar as componentes.
Passo 2
Para calcular as componentes vamos usar aquele macetinho esperto:
A componente que está COlada com o ângulo é igual ao módulo do vetor vezes o COsseno do ângulo. Já a componente que está SEparada do ângulo é igual ao módulo do vetor vezes o SEno do ângulo.
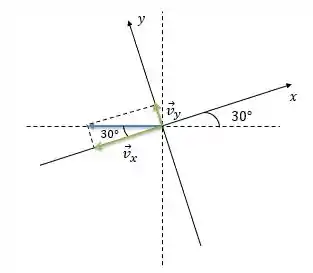
Nota que para a componente tem um sinal de negativo acompanhando. Esse sinal é pra indicar que essa componente está apontando no sentido contrário ao sentido do eixo . Beleza?
A questão nos deu o módulo do vetor:
E sabemos que:
Então, as componentes serão:
Lembrando que temos os vetores unitários e para representar as direções dos eixos e , respectivamente, podemos escrever o vetor assim:
Resposta