Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 13.1 - Ex. 65

Um sifão é um dispositivo para transferir um líquido de um recipiente para outro. O tubo mostrado na figura abaixo deve ser preenchido para iniciar o sifão, mas uma vez feito isso, o fluido fluirá através do tubo até que as superfícies do líquido nos recipientes estejam no mesmo nível. (a) Usando a equação de Bernoulli, mostre que a velocidade da água no tubo é 2 g d   (b) Qual é a pressão na parte mais alta do tubo?

Passo 1

a) Falaaa! Ele quer que a gente use Bernoulli para saber a velocidade dentro do tubo. Bernoulli diz que para um mesmo escoamento, temos uma relação entre entre 2 pontos diferentes do escoamento. Vale que

P 1 + ρ g z 1 + 1 2 ρ v 1 2 = P 2 + ρ g z 2 + 1 2 ρ v 2 2

Sendo que z é a altura do ponto em relação a um referencial, P é a pressão no ponto e v a velocidade nesse ponto.

Temos um sifão. Podemos fazer o esquema dele assim:

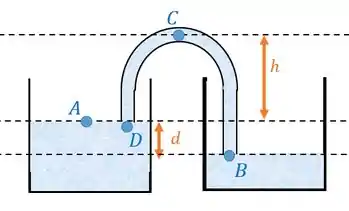
A água é transportada entre esses dois recipientes.

Podemos pensar que a velocidade dentro do tubo é a mesma em todos os pontos do tubo. Então, ali no ponto B , onde a água no tubo encontra a superfície de água no outro recipiente, teremos essa mesma velocidade que queremos encontrar.

Então aqui vamos encontrar v b , beleza?

Precisamos então comparar esse ponto B com outro ponto para usar Bernoulli. Vamos usar o ponto A porque ele está na superfície da água, e por isso vamos ter mais informações sobre ele. Vamos!

Passo 2

Assumindo que a altura do ponto C é H medindo do fundo dos containers, a equação de Bernoulli entre a superfície do container da esquerda e no ponto b fica:

P a t m + 1 2 ρ v a 2 + ρ g H - h = P a t m + 1 2 ρ v b 2 + ρ g H - h - d

A pressão dos dois é P a t m porque ambos estão na superfície de água, e nela temos a pressão atmosférica. Mesmo o ponto B que está dentro do tubo, porque podemos entender que simultaneamente ele está na superfície da água também.

v b queremos achar, mas quem é v a ? Essa é a velocidade na superfície da água v s u p e r f í c i e   fora do tudo. Podemos acha-la usando a equação da continuidade entre esse ponto e o ponto B :

v 1 A 1 = v 2 A 2

E para gente fica

v b A b = v s u p e r f i c i e A s u p e r f i c i e

v a = v s u p e r f i c i e = v b A b A s u p e r f i c i e

Essa A b é a área transversal do tubo, e A s u p e r f í c i e é a área transversal do container. Podemos observar que a área transversal do container é muito maior do que a área transversal do tubo, o que faz com que aquele denominador fique beemm grande.

Por isso, temos que v a = v s u p e r f i c i e = 0 aproximadamente.

Passo 3

Agora substituindo em Bernoulli

P a t m + 1 2 ρ v a 2 + ρ g H - h = P a t m + 1 2 ρ v b 2 + ρ g H - h - d

P a t m + ρ g H - h = P a t m + 1 2 ρ v b 2 + ρ g H - h - d

Simplificando

ρ g H - h = 1 2 ρ v b 2 + ρ g H - h - d

0 = 1 2 ρ v b 2 + ρ g - d

Isolando v b , temos que:

v b = 2 g d

Como ele pediu 😊

Passo 4

b) Para a letra b), vamos relacionar a pressão no mais alto ponto do tubo P t o p o com a pressão no ponto B :

P t o p o + 1 2 ρ v t o p o 2 + ρ g H = P a t m + 1 2 ρ v b 2 + ρ g H - h - d

Pensa comigo: o topo do tubo ainda é tubo né? Vimos que a velocidade é a mesma em todos os pontos do tubo, então a velocidade do topo vai ser igual a velocidade em B :

v t o p o = v b

Então

P t o p o + 1 2 ρ v b 2 + ρ g H = P a t m + 1 2 ρ v b 2 + ρ g H - h - d

Simplificando:

P t o p o + ρ g H = P a t m + ρ g ( H - h - d )

P t o p o = P a t m + ρ g ( - h - d )

P t o p o = P a t m - ρ g ( h + d )

Prontinho!

Obs: ficamos diferente do gabarito, mas está certinho, tudo bem?

Resposta

a) demonstração nos passos

b) P t o p o = P a t m - ρ g ( h + d )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pequeno orifício circular com diâmetro igual a 6,00 mm é cortado na superfície lateral de um grande tanque de água, a uma profundidade de 14,0 m abaixo da superfície. O topo do tanque está aberto p
Um sistema de irrigação de um campo de golfe descarrega água de um cano horizontal à taxa de 7 .200 c m 3 / s . Em um ponto do cano em que o raio é 4,0 cm, a pressão absoluta da água é 2,40 X 10 5 Pa.
Artéria obstruída. O sangue viscoso está escoando por uma artéria parcialmente obstruída pelo colesterol. Um cirurgião deseja remover uma quantidade suficiente do colesterol para dobrar a vazão de san
Entupimento da artéria. Uma cardiologista está tentando determinar qual porcentagem da artéria de um paciente está bloqueada por uma placa. Para fazer isso, ela mede a pressão sanguínea imediatamente
Uma bebida leve (essencialmente água) escoa em um tubo de uma fábrica de cerveja com vazão volumétrica tal que deve encher 220 latas de 355 ml por minuto. Em um ponto 2 do tubo, a pressão manométrica