Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 18.5 - Ex. 44
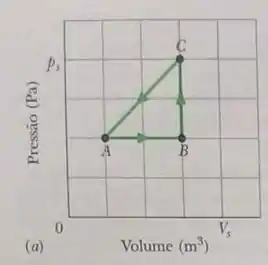
Um sistema termodinâmico passa do estado para o estado do estado B para o estado e de volta para o estado , como mostra o diagrama da Figura abaixo. A escala do eixo vertical é definida por e a escala do eixo horizontal é definida por . (a)-(g) Complete a tabela tabela da figura introduzindo um sinal positivo, um sinal negativo ou um zero na célula indicada (h) Qual e o trabalho realizado pelo sistema no ciclo
Passo 1
(a) e (b) Como comentamos em questões anteriores, lembrar-se de prestar atenção às Figuras e às informações dadas no enunciado é muito importante!
Beleza, então vamos lá completar a Tabela!
- : Primeiro, perceba que no processo o sistema está expandindo (o seu volume está aumentando). Então, o trabalho realizado pelo sistema sobre as suas vizinhanças, é positivo. Como a energia interna é igual a , sendo o calor transferido ao longo do processo, e, como diz a Tabela, , temos que também será um valor positivo, pois a soma de dois valores positivos sempre dará como resultado algo positivo!
- : Nesse trecho, podemos ver que o trabalho é nulo, pois a variação de volume nesse caso é igual a zero. Daí, temos que e, consequentemente, a variação de energia interna e o calor possuem o mesmo sinal. Então, nesse caso.
- Aqui, perceba que , pois a variação de volume é negativa.
Passo 2
(c) e (d)
Passo 3
(e) e (g)
Agora, para analisarmos o sinal de vamos usar uma estratégia mais ampla. Lembra que a variação de energia interna é uma função de estado, ou seja, que seu valor dependem apenas dos estados inicial e final? Pois é, nessa condição de função de estado, o cálculo de no caso em que o ponto inicial e final são iguais é igual a zero!
Mas como isso vai nos ajudar?
Já explico! Observe o ciclo completo: vimos que em , assim como em . Como é uma função de estado (só depende dos estados inicial e final), calculada no ciclo todo é igual a zero, pois nesse caso os estados final e inicial são os mesmos , e . Mas , para que a variação de energia interna no ciclo todo seja nula, é necessário que no trecho seja negativo para que a soma total seja nula.
Finalmente, como e são menores que zero e , então o calor trocado com as vizinhanças também é negativo.
Passo 2
(h) Para calcularmos o trabalho total, basta lembrarmos que ele é numericamente igual à área debaixo do gráfico que relaciona a pressão e o volume. Daí, basta calcularmos a área do triângulo indicado na figura, que é igual a
Mas calma! Qual deve ser o sinal do trabalho encontrado? Sempre que o ciclo estiver no sentido anti-horário ele é negativo e é positivo se for realizado no sentido horário. Então, nesse caso, temos que
Resposta
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)