Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.3 - Ex. 23

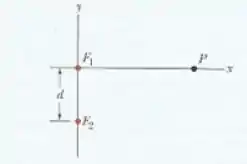
A figura mostra duas fontes pontuais e que emitem sons de comprimento de onda . As emissões são isotrópicas e em fase; a distância entre as fontes é . Em qualquer ponto sobre o eixo , as ondas produzidas por e interferem. Se está muito distante (), qual é (a) a diferença de fase entre as ondas produzidas por e e (b) o tipo de interferência que as ondas produzem? Suponha que o ponto é deslocado ao longo do eixo em direção a . (c) A diferença de fase entre as ondas aumenta ou diminui? A que distância da origem as ondas possuem uma diferença de fase de (d) , (e) e (f) ?

Passo 1

(a) Então, como vai ficar a interferência quando a distância de até as fontes tende ao infinito?

Olha, é importante entender o seguinte, como as duas são ondas sonoras, emitidas em fase com o mesmo comprimento de onda, a única coisa que pode tirá-las de fase é aquela distância entre elas.

Acontece que quando está muito longe das fontes, essa distância fica irrelevante (é como se você diminuísse muito o zoom na imagem, concorda que ia parecer que as duas fontes estão uma em cima da outra?).

Então beleza, nesse caso a diferença de fase é zero.

Passo 2

(b) Quando a diferença de fase é zero, a gente já sabe que a interferência é construtiva.

E é isso que vai acontecer nesse caso.

Passo 3

Bom, quando nos aproximamos das fontes, a distância entre elas passa a ser significativa, ou seja, passa a ser possível ver alguma diferença de fase.

Como antes (“no infinito”) ela com certeza era zero, podemos dizer que esse movimento corresponde a um aumento da diferença de fase, mesmo que haja alguns pontos próximos da origem onde a diferença vai ser zero novamente.

Passo 4

Para as próximas perguntas, vamos precisar achar uma fórmula pra calcular a diferença de fase :

A distância é o mais difícil de calcular. Vamos tentar escrever ela em função de , que é a posição do ponto no eixo horizontal.

Pra fazer a distância entre e até que é bem tranquilo:

E pra fazer a distância entre e , é só usar o teorema de Pitágoras:

Ok, agora o vai ser:

E o comprimento de onda já foi dado no enunciado:

Então:

Passo 5

(d) Agora vamos tomar cuidado, porque o enunciado está meio estranho.

Nesse item ele pede o valor de que gera a diferença de fase , mas estamos acostumados a falar de diferenças de fase em radianos. E a fórmula que a gente achou faz justamente isso.